题目内容
6. 如图,AE∥CF,AE=CF,点E、F在线段BD上,且BF=DE,连接AB、DC.求证:AB∥CD.
如图,AE∥CF,AE=CF,点E、F在线段BD上,且BF=DE,连接AB、DC.求证:AB∥CD.
分析 由平行的性质可得∠AEB=∠CFD,结合条件可证明△AEB≌△CFD,可得到∠B=∠D,可证明AB∥CD.
解答 证明:
∵AE∥CF,
∴∠AEB=∠CFD,
∵BF=DE,
∴BE=FD,
在△AEB和△CFD中
$\left\{\begin{array}{l}{AE=CF}\\{∠AEB=∠CFD}\\{BE=DF}\end{array}\right.$
∴△AEB≌△CFD(SAS),
∴∠B=∠D,
∴AB∥CD.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列说法正确的是( )
| A. | $\sqrt{81}$的平方根是±9 | B. | $\sqrt{64}$的立方根是±2 | ||
| C. | x为任意数都有$\root{3}{{x}^{3}}$=x | D. | 16的平方根是4 |
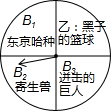 周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)
周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)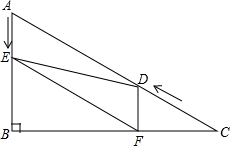 如图,在Rt△ABC中,∠B=90°,AB=3,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AB=3,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.