题目内容
16.已知二次函数y=-$\frac{1}{2}$x2-x+$\frac{3}{2}$(1)直接写出这个函数的图象与x轴交点的坐标;
(2)写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
分析 (1)令y=0得到关于x的一元二次方程,然后求得方程的解,从而得到图象与x轴交点的坐标;
(2)根据抛物线与x轴交点的坐标以及抛物线的增减性可判断;
(3)根据平移与坐标变换的关系求解即可.
解答 解:(1)令y=0得:-$\frac{1}{2}$x2-x+$\frac{3}{2}$=0,
整理得:x1=-3,x2=1.
∴函数图象与x轴交点的坐标为(-3,0)和(1,0).
(2)∵函数图象与x轴交点的坐标为(-3,0)和(1,0).
∴抛物线的对称轴为x=-1.
∵a=-$\frac{1}{2}$<0,
∴当x<-1时,y随x的增大而增大,当x>-1时,y随x的增大而减小.
∴当y<0时,x的取值范围是x<-3或x>1.
(3)图象沿x轴向右平移3个单位后的解析式为y=-$\frac{1}{2}$(x-3)2-(x-3)+$\frac{3}{2}$,
整理得:y=$-\frac{1}{2}{x}^{2}+2x$.
点评 本题主要考查的是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解题的关键.

练习册系列答案
相关题目
6.将多项式-2x-x3+2x2+5按降幂排列,正确的是( )
| A. | x3-2x+2x2+5 | B. | 5-2x+2x2-x3 | C. | -x3+2x2+2x+5 | D. | -x3+2x2-2x+5 |
7.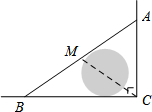 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )| A. | 0.5km | B. | 0.6km | C. | 0.9km | D. | 1.2km |
 如果有理数a、b、c在数轴上的位置如图所示,
如果有理数a、b、c在数轴上的位置如图所示, 如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).
如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).