题目内容
观察下列等式:12=1,22=4,32=9,42=16,52=25,…,那么12+22+32+42+…+20142的个位数字是 .
考点:尾数特征
专题:
分析:由题中可以看出,故个位的数字是以10为周期变化的,用2014÷10,计算一下看看有多少个周期即可.
解答:解:以2为指数的幂的末位数字是1,4,9,6,5,6,9,4,1,0依次循环的,
∵2014÷10=201…4,
(1+4+9+6+5+6+9+4+1+0)×201+(1+4+9+6)
=45×201+20
=9045+20
=9065,
∴12+22+32+42+…+20142的个位数字是5.
故答案为:5.
∵2014÷10=201…4,
(1+4+9+6+5+6+9+4+1+0)×201+(1+4+9+6)
=45×201+20
=9045+20
=9065,
∴12+22+32+42+…+20142的个位数字是5.
故答案为:5.
点评:此题主要考查了找规律,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解决本题的关键是找到以2为指数的末位数字的循环规律.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列命题错误的是( )
A、若 a<1,则(a-1)
| ||||||
B、若
| ||||||
| C、依次连接菱形各边中点得到的四边形是矩形 | ||||||
D、
|
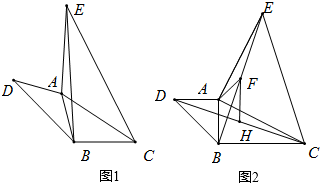 AB,AC=AE,∠DAB=∠CAE,连接DC与BE.
AB,AC=AE,∠DAB=∠CAE,连接DC与BE.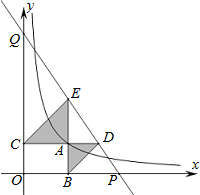 如图,已知动点A在函数
如图,已知动点A在函数