题目内容
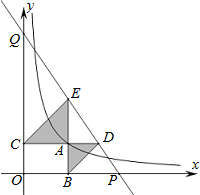 如图,已知动点A在函数y=
如图,已知动点A在函数y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:计算题
分析:作EM⊥y轴于M,DN⊥x轴于N,如图,设A点坐标为(a,b),则AC=AE=a,AB=AD=b,先证明Rt△QME∽Rt△DNP,利用相似比表示出PN=
a,QM=
b,再证明△QME∽△QCD,利用相似比得到
=
,则a2=
b2,然后根据
a2+
b2=13,可得到
b2+b2=26,解得b=2
,再计算出a的值,最后利用k=ab求解.
| 4 |
| 9 |
| 9 |
| 4 |
| ||
|
| a |
| a+b |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 2 |
解答:解: 作EM⊥y轴于M,DN⊥x轴于N,如图,设A点坐标为(a,b),则AC=AE=a,AB=AD=b,
作EM⊥y轴于M,DN⊥x轴于N,如图,设A点坐标为(a,b),则AC=AE=a,AB=AD=b,
∵ME∥OP,
∴∠QEM=∠DPN,
∴Rt△QME∽Rt△DNP,
∴
=
=
=
,
∴PN=
a,QM=
b,
∵ME∥CD,
∴△QME∽△QCD,
∴
=
,即
=
,
∴a2=
b2,
∴图中阴影部分的面积等于13时,∵图中阴影部分的面积等于13,即
a2+
b2=13,
∴
b2+b2=26,解得b=2
,
∴a2=
×8=18,解得a=3
,
∴k=ab=3
×2
=12.
故答案为12.
 作EM⊥y轴于M,DN⊥x轴于N,如图,设A点坐标为(a,b),则AC=AE=a,AB=AD=b,
作EM⊥y轴于M,DN⊥x轴于N,如图,设A点坐标为(a,b),则AC=AE=a,AB=AD=b,∵ME∥OP,
∴∠QEM=∠DPN,
∴Rt△QME∽Rt△DNP,
∴
| QM |
| DN |
| ME |
| PN |
| QE |
| DP |
| 9 |
| 4 |
∴PN=
| 4 |
| 9 |
| 9 |
| 4 |
∵ME∥CD,
∴△QME∽△QCD,
∴
| QM |
| QC |
| ME |
| CD |
| ||
|
| a |
| a+b |
∴a2=
| 9 |
| 4 |
∴图中阴影部分的面积等于13时,∵图中阴影部分的面积等于13,即
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 9 |
| 4 |
| 2 |
∴a2=
| 9 |
| 4 |
| 2 |
∴k=ab=3
| 2 |
| 2 |
故答案为12.
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.也考查了相似三角形的判定与性质.
| k |
| x |
| k |
| x |

练习册系列答案
相关题目
下列各式中不能用平方差公式计算的是( )
| A、(-x+y)(-x-y) |
| B、(a-2b)(2b+a) |
| C、(a-b)(a+b)(a2+b2) |
| D、(a+b-c)(a+b-c) |