题目内容
如图1,已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=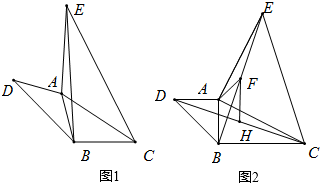 AB,AC=AE,∠DAB=∠CAE,连接DC与BE.
AB,AC=AE,∠DAB=∠CAE,连接DC与BE.
(1)求证:△DAC≌△BAE;
(2)F、H分别是BE与DC的中点;
①如图2.当∠DAB=∠CAE=90°时,求∠AFH的度数;
②请探究当∠DAB等于多少度时,AF=FH?请说明理由.
 AB,AC=AE,∠DAB=∠CAE,连接DC与BE.
AB,AC=AE,∠DAB=∠CAE,连接DC与BE.(1)求证:△DAC≌△BAE;
(2)F、H分别是BE与DC的中点;
①如图2.当∠DAB=∠CAE=90°时,求∠AFH的度数;
②请探究当∠DAB等于多少度时,AF=FH?请说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)求出∠DAC=∠BAE,然后利用“边角边”证明即可;
(2)①连接AH,根据全等三角形对应角相等可得∠AEB=∠ACD,全等三角形对应边相等可得BE=CD,然后求出EF=CH,再利用“边角边”证明△ACH和△AEF全等,根据全等三角形对应边相等可得AF=AH,全等三角形对应角相等可得∠EAF=∠CAH,然后求出∠FAH=∠CAE,再根据等腰三角形两底角相等列式计算即可得解;
②判断出△AFH是等边三角形,然后根据等边三角形的三个角都是60°求解即可.
(2)①连接AH,根据全等三角形对应角相等可得∠AEB=∠ACD,全等三角形对应边相等可得BE=CD,然后求出EF=CH,再利用“边角边”证明△ACH和△AEF全等,根据全等三角形对应边相等可得AF=AH,全等三角形对应角相等可得∠EAF=∠CAH,然后求出∠FAH=∠CAE,再根据等腰三角形两底角相等列式计算即可得解;
②判断出△AFH是等边三角形,然后根据等边三角形的三个角都是60°求解即可.
解答:(1)证明:∵∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS);
(2)解:①如图,连接AH,
∵△DAC≌△BAE,
∴∠AEB=∠ACD,BE=CD,
∵F、H分别是BE与DC的中点,
∴EF=
BE,CH=
CD,
∴EF=CH,
在△ACH和△AEF中,
,
∴△ACH≌△AEF(SAS),
∴AF=AH,∠EAF=∠CAH,
∴∠FAH=∠CAE,
∵∠DAB=∠CAE=90°,
∴∠AFH=
(180°-90°)=45°;
②由①可知,AF=AH,∠FAH=∠CAE=∠DAB,
∵AF=FH,
∴AF=AH=FH,
∴△AFH是等边三角形,
∴∠FAH=60°,
∴∠DAB=60°.
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△DAC和△BAE中,
|
∴△DAC≌△BAE(SAS);
(2)解:①如图,连接AH,
∵△DAC≌△BAE,
∴∠AEB=∠ACD,BE=CD,
∵F、H分别是BE与DC的中点,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |

∴EF=CH,
在△ACH和△AEF中,
|
∴△ACH≌△AEF(SAS),
∴AF=AH,∠EAF=∠CAH,
∴∠FAH=∠CAE,
∵∠DAB=∠CAE=90°,
∴∠AFH=
| 1 |
| 2 |
②由①可知,AF=AH,∠FAH=∠CAE=∠DAB,
∵AF=FH,
∴AF=AH=FH,
∴△AFH是等边三角形,
∴∠FAH=60°,
∴∠DAB=60°.
点评:本题考查了全等三角形的判定与性质,等腰三角形两底角相等的性质,等边三角形的判定与性质,熟练掌握三角形全等的判断方法并准确识图是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,菱形ABCD的对角线AC和BD相交于点O,求证:S菱形ABCD=
如图,菱形ABCD的对角线AC和BD相交于点O,求证:S菱形ABCD=