题目内容
9.在学习二次根式时,发现一些含有根号的式子可以化成另一式子的平方,如:$5+2\sqrt{6}=(2+3)+2\sqrt{2×3}={(\sqrt{2})^2}+{(\sqrt{3})^2}+2\sqrt{2}•\sqrt{3}={(\sqrt{2}+\sqrt{3})^2}$$8-2\sqrt{15}=(5+3)-2\sqrt{5×3}={(\sqrt{5})^2}+{(\sqrt{3})^2}-2\sqrt{5}×\sqrt{3}={(\sqrt{5}-\sqrt{3})^2}$(1)请你按照上述方法将$10+2\sqrt{21}$化成一个式子的平方.
(2)将下列等式补充完整$a+b-2\sqrt{ab}$=($\sqrt{a}$-$\sqrt{b}$)2(a≥0 b≥0),并证明这个等式.
(3)若$a+2\sqrt{15}={(\sqrt{m}+\sqrt{n})^2}$且a、m、n均为正整数,则a=8或16.
分析 (1)利用题中的方法,把10分成7与3的和,把21分成7与3的积,然后利用完全平方公式写成平方式即可;
(2)把a和b写成($\sqrt{a}$)2与($\sqrt{b}$)2,然后利用完全平方公式写成平方式即可;
(3)利用完全平方公式把等式右边展开,则m+n=a,mn=15,然后利用有理数的整除性确定m和n的值,再计算对应的a的值.
解答 解:(1)10+2$\sqrt{21}$=7+2$\sqrt{21}$+3=($\sqrt{7}$)2+2$\sqrt{7}$•$\sqrt{3}$+($\sqrt{3}$)2=($\sqrt{7}$+$\sqrt{3}$)2;
(2)$a+b-2\sqrt{ab}$=($\sqrt{a}$-$\sqrt{b}$)2;
证明如下:$a+b-2\sqrt{ab}$=($\sqrt{a}$)2+($\sqrt{b}$)2-2$\sqrt{a}$•$\sqrt{b}$=($\sqrt{a}$-$\sqrt{b}$)2;
(3)∵$a+2\sqrt{15}={(\sqrt{m}+\sqrt{n})^2}$,
∴a+2$\sqrt{15}$=m+2$\sqrt{mn}$+n,
∴m+n=a,mn=15,
而a、m、n均为正整数,
∴m与n的值为3和5或1和15,
∴a的值为8或16.
故答案为($\sqrt{a}$-$\sqrt{b}$)2;8或16.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
20.计算(-3a-bc)•(bc-3a)的结果等于( )
| A. | bc2-9a2 | B. | b2c2-3a2 | C. | 9a2-b2c2 | D. | b2c2-9a2 |
4.下列选项中的三条线段的长度,能组成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 4,6,8 | D. | 5,5,11 |
14.下列乘法中,不能运用平方差公式进行计算的是( )
| A. | (x+a)(x-a) | B. | (a+b)(-a-b) | C. | (-x-b)(x-b) | D. | (b+m) (m-b) |
19.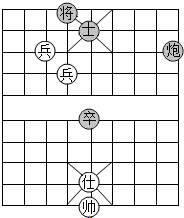 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )| A. | (8,7) | B. | (0,4) | C. | (0,0) | D. | (4,0) |
 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.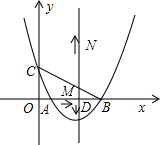 △ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.
△ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.