题目内容
7.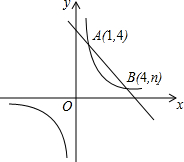 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.(1)求反比例函数和一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤$\frac{m}{x}$的解集.
(3)点P是x轴上的一点,且使PA+PB最小,求△ABP的面积.
分析 (1)将点A(1,4)代入反比例函数解析式可得其解析式;先根据反比例函数解析式求得点B坐标,再由A、B坐标可得直线解析式;
(2)根据图象得出不等式kx+b≤$\frac{m}{x}$的解集即可;
(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,根据B的坐标求得B′的坐标,然后根据待定系数法求得直线AB′的解析式,进而求得与x轴的交点P,再求面积即可.
解答 解:(1)把A(1,4)代入y=$\frac{m}{x}$,得:m=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
把B(4,n)代入y=$\frac{4}{x}$,得:n=1,
∴B(4,1),
把A(1,4)、(4,1)代入y=kx+b,得:$\left\{\begin{array}{l}{k+b=4}\\{4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴一次函数的解析式为y=-x+5;
(2)根据图象得当0<x≤1或x≥4,一次函数y=-x+5的图象在反比例函数y=$\frac{4}{x}$的下方;
∴kx+b≤$\frac{m}{x}$的解集为0<x≤1或x≥4;
(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,
∵B(4,1),
∴B′(4,-1),
设直线AB′的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{m+n=4}\\{4m+n=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{5}{3}}\\{n=\frac{17}{3}}\end{array}\right.$,
∴直线AB′的解析式为y=-$\frac{5}{3}$x+$\frac{17}{3}$,
令y=0,得-$\frac{5}{3}$x+$\frac{17}{3}$=0,
解得x=$\frac{17}{5}$,
∴点P的坐标为($\frac{17}{5}$,0),
∴S△ABP=$\frac{(1+4)×3}{2}$-$\frac{4×\frac{12}{5}}{2}$$\frac{1×\frac{1}{5}}{2}$=$\frac{12}{5}$.
点评 本题主要考查反比例函数和一次函数的交点及待定系数法求函数解析式、轴对称-最短路线问题,掌握图象的交点的坐标满足两个函数解析式是解题的关键.


| A. | A→B→C→A | B. | A→B→C→D | C. | A→D→O→A | D. | A→O→B→C |
| A. | a2•a3=a6 | B. | (ab)2=a2b2 | C. | (a2)3=a5 | D. | a6÷a2=a3 |
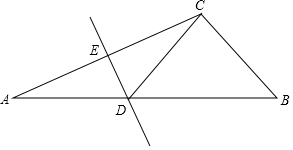 如图,在△ABC中,∠ACB=111°,AC边上的垂直平分线交AB于点D,交AC边于点E,连接CD.
如图,在△ABC中,∠ACB=111°,AC边上的垂直平分线交AB于点D,交AC边于点E,连接CD.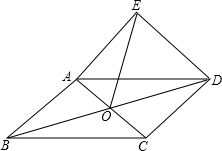 如图,在平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,把△OAB沿对角线AC翻折后,E与B对应.
如图,在平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,把△OAB沿对角线AC翻折后,E与B对应.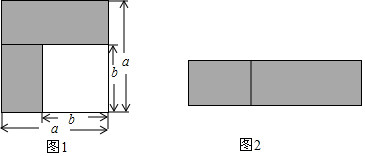
 已知,如图,△ABC,射线AM平分∠BAC
已知,如图,△ABC,射线AM平分∠BAC