题目内容
17.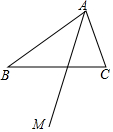 已知,如图,△ABC,射线AM平分∠BAC
已知,如图,△ABC,射线AM平分∠BAC(1)尺规作图(不写作法,保留作图痕迹)
作BC的中垂线,与AM相交于G,连接BG,CG
(2)在(1)的条件下,∠BAC+∠BGC=180度.
分析 (1)如图所示,作出线段BC的垂直平分线即可;
(2)如图作GF⊥AC于F,GE⊥AB于E,只要证明△GEB≌△GFC,推出∠EGB=∠CGF,推出∠BGC=∠EGF,由∠EGF+∠BAC=360°-90°-90°=180°,可得∠BGC+∠BAC=180°;
解答 解:(1)如图所示,直线DG即为所求.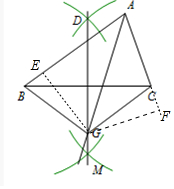
(2)如图作GF⊥AC于F,GE⊥AB于E,
∵GA平分∠BAC,
∵GF=GE,
∵DG垂直平分线段BC,
∴BG=GC,
在Rt△HEB和Rt△GFC中,
$\left\{\begin{array}{l}{GB=GC}\\{GE=GF}\end{array}\right.$,
∴Rt△GEB≌Rt△GFC,
∴∠EGB=∠CGF,
∴∠BGC=∠EGF,
∵∠EGF+∠BAC=360°-90°-90°=180°,
∴∠BGC+∠BAC=180°,
故答案为180°.
点评 本题考查作图-基本作图、角平分线的性质定理、全等三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题.

练习册系列答案
相关题目
4.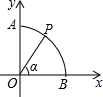 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (sinα,cosα) | D. | (cosα,sinα) |
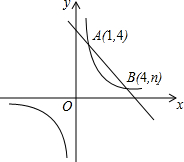 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点. 如图,已知CD∥BF,∠B+∠D=180°,求证:AB∥DE.
如图,已知CD∥BF,∠B+∠D=180°,求证:AB∥DE.