题目内容
12.乘法公式的探究及应用.(1)如图1,可以求出阴影部分的面积是a2-b2(写成两数平方差的形式);若将阴影部分裁剪下来,重新拼成一个矩形,如图2,它的面积是(a+b)(a-b)(写成多项式乘法的形式),比较左、右两图的阴影部分的面积,可以得到乘法公式(a+b)(a-b)=a2-b2(用式子表达)
(2)计算:(a+b-c)(a-b+c)
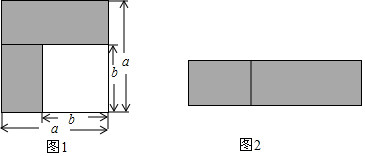
分析 (1)根据面积的和差关系以及矩形面积公式,即可得到阴影部分的面积的表达式,进而得出公式;
(2)先将原式化为[a+(b-c)][a-(b-c)],再利用(1)中的公式进行计算即可.
解答 解:(1)如图1,根据阴影部分的面积等于大正方形的面积减去小正方形的面积,可得阴影部分的面积是a2-b2,
如图2,根据矩形的长为a+b,宽为a-b,可得矩形的面积是:(a+b)(a-b),
根据图中阴影部分面积线段,可以得到公式:(a+b)(a-b)=a2-b2,
故答案是:a2-b2,(a+b)(a-b),(a+b)(a-b)=a2-b2;
(2)解:原式=[a+(b-c)][a-(b-c)]
=a2-(b-c)2
=a2-b2+2bc-c2.
点评 本题主要考查了平方差公式的几何背景,解决问题的关键是依据数形结合思想进行求解.解题时注意平方差公式的结构特征.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.圆锥的体积是120立方分米,底面积是10平方分米,高是( )分米.
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
3.已知正三角形的边长为2,则它的内切圆和外接圆组成的圆环面积为( )
| A. | 3π | B. | 2π | C. | π | D. | $\frac{1}{2}$π |
4.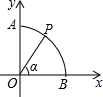 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (sinα,cosα) | D. | (cosα,sinα) |
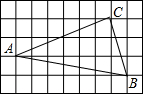 如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.
如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.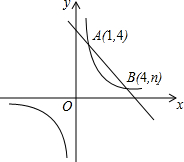 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.

 已知直线y=-x+4.
已知直线y=-x+4.