题目内容
6.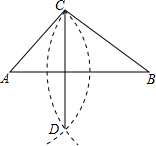 已知△ABC,按如下步骤作图:
已知△ABC,按如下步骤作图:(1)以点A为圆心,以AC的长为半径画弧;
(2)以点B为圆心,以BC的长为半径画弧,与前一段弧相交于点D;
(3)连接CD,
若AC=5,BC=CD=8.则AB的长是( )
| A. | 3+2$\sqrt{3}$ | B. | 10 | C. | 3+4$\sqrt{3}$ | D. | 12 |
分析 利用基本作图方法可得出AB垂直平分DC,进而利用勾股定理得出AO,BO的长,进而得出答案.
解答  解:由题意可得:AB垂直平分DC,
解:由题意可得:AB垂直平分DC,
∵BC=CD=8,
∴CO=DO=4,
∴BO=$\sqrt{B{C}^{2}-C{O}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵AC=5,CO=4,
∴AO=3,
∴AB=3+4$\sqrt{3}$.
故选:C.
点评 此题主要考查了基本作图以及勾股定理,正确得出AB垂直平分DC是解题关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
17.定义三角 表示3abc,方框
表示3abc,方框 表示xz+wy,则
表示xz+wy,则 ×
× 的结果为( )
的结果为( )
 表示3abc,方框
表示3abc,方框 表示xz+wy,则
表示xz+wy,则 ×
× 的结果为( )
的结果为( )| A. | 72m2n-45mn2 | B. | 72m2n+45mn2 | C. | 24m2n-15mn2 | D. | 24m2n+15mn2 |
14.在下列说法中是错误的是( )
| A. | 在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形 | |
| B. | 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形 | |
| C. | 在△ABC中,若a=$\frac{3}{5}$c,b=$\frac{4}{5}$c,则△ABC为直角三角形 | |
| D. | 在△ABC中,若a:b:c=2:2:4,则△ABC为直角三角形 |
1. 如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )
如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )
 如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )
如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )| A. | n+2 | B. | n+3 | C. | 2n-1 | D. | 2n+1 |
11.设n为正整数,且6<$\sqrt{n}$<7,则n可能为( )
| A. | 25 | B. | 28 | C. | 43 | D. | 58 |
18. 在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
 在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )| A. | 3 | B. | 4 | C. | 1.5 | D. | 2 |
15.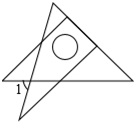 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )| A. | 60° | B. | 75° | C. | 65° | D. | 70° |
16.在△ABC中,若∠BAC=90°,则( )
| A. | BC=AB+AC | B. | AC2=AB2+BC2 | C. | AB2=AC2+BC2 | D. | BC2=AB2+AC2 |