题目内容
18．
在△ABC中∠B=30°，AB=4，BC=3，则S△ABC=（ ）| A． | 3 | B． | 4 | C． | 1.5 | D． | 2 |
分析 作BC边上的高AD，根据直角三角形30°所对的直角边等于斜边的一半，求出AD，根据三角形的面积公式即可求出．
解答 
解：如图，过A作AD⊥BC于D，
∵AB=4，∠B=30°，
∴AD=$\frac{1}{2}$AB=2，
又BC=3，
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×3×2=3．
故选A．
点评 本题考查了30°角所对的直角边等于斜边的一半的性质，三角形的面积公式，熟记直角三角形的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
8．
如图，∠2+∠3=180°，∠4=80°，则∠1=（ ）
如图，∠2+∠3=180°，∠4=80°，则∠1=（ ）| A． | 70° | B． | 110° | C． | 100° | D． | 80° |
9．若3×9k=311，则k的值为（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
6．
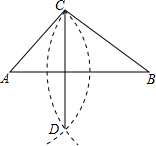已知△ABC，按如下步骤作图：
（1）以点A为圆心，以AC的长为半径画弧；
（2）以点B为圆心，以BC的长为半径画弧，与前一段弧相交于点D；
（3）连接CD，
若AC=5，BC=CD=8．则AB的长是（ ）
已知△ABC，按如下步骤作图：（1）以点A为圆心，以AC的长为半径画弧；
（2）以点B为圆心，以BC的长为半径画弧，与前一段弧相交于点D；
（3）连接CD，
若AC=5，BC=CD=8．则AB的长是（ ）
| A． | 3+2$\sqrt{3}$ | B． | 10 | C． | 3+4$\sqrt{3}$ | D． | 12 |
13．
如图，在△ABC中，AB=8，BC=10，AC=6，则BC边上的高AD为（ ）
如图，在△ABC中，AB=8，BC=10，AC=6，则BC边上的高AD为（ ）| A． | 8 | B． | 9 | C． | $\frac{24}{5}$ | D． | 10 |
如图，学校有一块长方形花坛，有极少数人为了避开拐角走“捷径”，在花坛内走出了一条“路”，他们仅仅少走了（ ）步，却踩伤了花草（假设2步为1米）
7．一组按规律排列的式子：a2，$\frac{{a}^{4}}{3}$，$\frac{{a}^{6}}{5}$，$\frac{{a}^{8}}{7}$，…，则第2016个式子是（ ）
| A． | $\frac{{a}^{2016}}{2015}$ | B． | $\frac{{a}^{2016}}{4029}$ | C． | $\frac{{a}^{4032}}{4031}$ | D． | $\frac{{a}^{4032}}{4029}$ |
8．
A，B，C三个车站在东西笔直的一条公路上，现要建一个加油站使其到三个车站的距离和最小，则加油站应建在（ ）
A，B，C三个车站在东西笔直的一条公路上，现要建一个加油站使其到三个车站的距离和最小，则加油站应建在（ ）| A． | 在A的左侧 | B． | 在AB之间 | C． | 在BC之间 | D． | B处 |