题目内容

1．如图，用火柴棍拼成一排由三角形组成的图形．若拼成的图形中有n个三角形，则需要火柴棍的根数是（　　）
A．n+2B．n+3C．2n-1D．2n+1

分析 对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，从而得出答案．

解答 解：∵第一个三角形需要三根火柴棍，再每增加一个三角形就增加2根火柴棒，
∴有n个三角形，则需要2n+1根火柴棍；
故选D．

点评 此题主要考查了学生通过特例分析从而归纳总结出一般结论的能力，关键是找出图中变化的规律．

练习册系列答案
相关题目
11．某书每本定价8元，若购书不超过10本，按原价付款；若一次购书10本以上，超过10本部分按八折付款．设一次购书数量为x本（x＞10），则付款金额为（　　）
A．6.4x元B．（6.4x+80）元C．（6.4x+16）元D．（144-6.4x）元
12．一个图形的各点纵坐标乘以2，横坐标不变，这个图形发生的变化是（　　）
A．横向拉伸为原来的2倍B．纵向拉伸为原来的2倍
C．横向压缩为原来的$\frac{1}{2}$D．纵向压缩为原来的$\frac{1}{2}$
9．若3×9k=311，则k的值为（　　）
A．5B．4C．3D．2
16．如图，∠1=∠2，∠3=80°，则∠4=（　　）
A．100°B．110°C．120°D．130°
6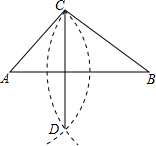．已知△ABC，按如下步骤作图：
（1）以点A为圆心，以AC的长为半径画弧；
（2）以点B为圆心，以BC的长为半径画弧，与前一段弧相交于点D；
（3）连接CD，
若AC=5，BC=CD=8．则AB的长是（　　）
A．3+2$\sqrt{3}$B．10C．3+4$\sqrt{3}$D．12
13．如图，在△ABC中，AB=8，BC=10，AC=6，则BC边上的高AD为（　　）
A．8B．9C．$\frac{24}{5}$D．10
10．在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲移到一边，花朵齐及水面，已知红莲移动的水平距离为2米，这里的水深为（　　）米．
A．1.5B．2C．2.5D．1
11．已知a-b=3，则代数式a2-b2-6b的值为（　　）
A．3B．6C．9D．12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网