题目内容
7．用正四边形和正三角形可以做平面镶嵌，下面就是用正四边形和正三角形镶嵌出的一组图案，按此规律，第n个图案中正三角形的个数为3n（用含n的代数式表示）
分析 由题意可知：第（1）个图案有3×1=3个三角形，第（2）个图案有3×2=6个三角形，第（3）个图案有3×3=9个三角形，…依此规律，第n个图案有3n个三角形．
解答 解：∵第（1）个图案有3×1=3个三角形，
第（2）个图案有3×2=6个三角形，
第（3）个图案有3×3=9个三角形，
…
∴第n个图案有3n个三角形．
故答案为：3n；
点评 此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．
练习册系列答案
相关题目
如图，已知?OABC的顶点A、C分别在直线x=2和x=6上，O是坐标原点，则对角线OB长的最小值为8．
18．某校“棋乐无穷”社团前两次购买的两种材质的象棋采购如下表（近期两种材质象棋的售价一直不变）；
（1）若该社团计划再采购这两种材质的象棋各5盒，则需要多少元？
（2）若该社团准备购买这两种材质的象棋共50盒，且要求塑料象棋的数量不多于玻璃象棋数量的3倍，请设计出最省钱的购买方案，并说明理由．
| 塑料象棋 | 玻璃象棋 | 总价（元） | |
| 第一次（盒） | 1 | 3 | 26 |
| 第二次（盒） | 3 | 2 | 29 |
（2）若该社团准备购买这两种材质的象棋共50盒，且要求塑料象棋的数量不多于玻璃象棋数量的3倍，请设计出最省钱的购买方案，并说明理由．
15．
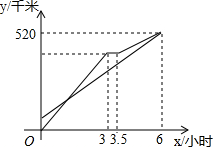甲、乙两车从A地出发沿同一路线驶向B地，甲车匀速驶向B地，甲车出发30分钟后，乙车才出发，乙先匀速行驶一段时间后，到达货站装货后继续行驶，速度减少了56千米/时，结果与甲车同时到达B地，甲乙两车距A地的路程y（千米）与乙车行驶时间x（时）之间的函数图象如图所示，下列说法中正确的是（ ）
甲、乙两车从A地出发沿同一路线驶向B地，甲车匀速驶向B地，甲车出发30分钟后，乙车才出发，乙先匀速行驶一段时间后，到达货站装货后继续行驶，速度减少了56千米/时，结果与甲车同时到达B地，甲乙两车距A地的路程y（千米）与乙车行驶时间x（时）之间的函数图象如图所示，下列说法中正确的是（ ）| A． | 甲车从A地到B地行驶了6小时 | |
| B． | 甲的速度是120千米/时 | |
| C． | 乙出发90分钟追上甲 | |
| D． | 当两车在行驶过程中，相距40千米时，x=2或3.5 |
2．
如图所示，△ABC中，DE∥BC，AC=9，CE=6，AD=4，则BD的值为（ ）
如图所示，△ABC中，DE∥BC，AC=9，CE=6，AD=4，则BD的值为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
19．
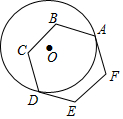如图，半径为1的⊙O与正六边形ABCDEF相切于点A、D，则$\widehat{AD}$的长为（ ）
如图，半径为1的⊙O与正六边形ABCDEF相切于点A、D，则$\widehat{AD}$的长为（ ）| A． | $\frac{1}{6}$π | B． | $\frac{1}{3}$π | C． | $\frac{2}{3}$π | D． | $\frac{5}{6}$π |
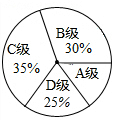为了解某区3600名九年级学生的体育训练情况，随机抽取了区内200名九年级学生进行了一次体育模拟测试，把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格，并将测试结果绘成了如图所示的统计图，由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人．
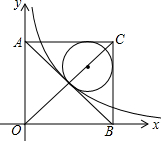如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为（6-3$\sqrt{2}$）的圆内切于△ABC，则k的值为9．