题目内容
17.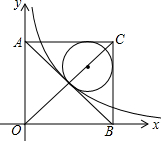 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.
分析 设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N,设圆心为Q,切点为H、E,连接QH、QE.根据正方形的性质得出AD=BD=DO=CD、NO=DN、HQ=QE、HC=CE,根据半径为(6-3$\sqrt{2}$)的圆内切于△ABC,得出CD的长,从而得出DO的长,再利用勾股定理求出NO2的值,结合反比例函数图象上点的坐标特征即可求出k值.
解答 解:设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N,设圆心为Q,切点为H、E,连接QH、QE.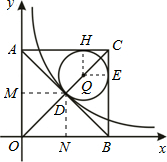
∵在正方形AOBC中,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,
∴AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,
∵QH⊥AC,QE⊥BC,∠ACB=90°,
∴四边形HQEC是正方形.
∵半径为(6-3$\sqrt{2}$)的圆内切于△ABC,
∴DO=CD.
∵HQ2+HC2=QC2,
∴2HQ2=QC2=2×(6-3$\sqrt{2}$)2,
∴QC2=108-72$\sqrt{2}$=(6$\sqrt{2}$-6)2,
∴QC=6$\sqrt{2}$-6,
∴CD=6$\sqrt{2}$-6+(6-3$\sqrt{2}$)=3$\sqrt{2}$,
∴DO=3$\sqrt{2}$.
∵NO2+DN2=DO2=(3$\sqrt{2}$)2=18,
∴2NO2=18,
∴NO2=9,
∴DN•NO=9,
即:xy=k=9.
故答案为9.
点评 本题考查了反比例函数图象上点的坐标特征、正方形的性质以及三角形的内切圆及圆心,根据已知求出CD的长度,进而得出DN×NO=9是解决问题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
8.《2017中国共享单车行业研究报告》报告指出,2月20日至26日一周,摩拜单车的日均有效使用时间是1100万分钟,远远领先行业第二名ofo共享单车,使用量稳居行业首位,数字1100万用科学记数法表示为( )
| A. | 0.11×108 | B. | 1.1×108 | C. | 0.11×107 | D. | 1.1×107 |
1.若∠AOB=90°,∠BOC=40°,则∠AOC的度数为( )
| A. | 50° | B. | 50° 或120° | C. | 50°或130° | D. | 130° |

 如图,一次函数y=x+b的图象过点A(1,2),且与x轴相交于点B,若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).
如图,一次函数y=x+b的图象过点A(1,2),且与x轴相交于点B,若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).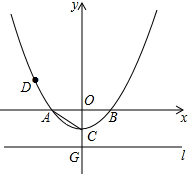 如图,在以O为坐标原点的平面直角坐标系中,二次函数y=$\frac{1}{4}$x2+bx+c 的图象与x轴交于A,B两点,与y轴交于点C(0,-1).连结AC,tan∠OCA=2,直线l 过点G(0,-2)且平行于x轴.
如图,在以O为坐标原点的平面直角坐标系中,二次函数y=$\frac{1}{4}$x2+bx+c 的图象与x轴交于A,B两点,与y轴交于点C(0,-1).连结AC,tan∠OCA=2,直线l 过点G(0,-2)且平行于x轴. 如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.