题目内容
17. 如图,已知?OABC的顶点A、C分别在直线x=2和x=6上,O是坐标原点,则对角线OB长的最小值为8.
如图,已知?OABC的顶点A、C分别在直线x=2和x=6上,O是坐标原点,则对角线OB长的最小值为8.
分析 过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E.则OB=$\sqrt{O{E}^{2}+B{E}^{2}}$.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.
解答 解: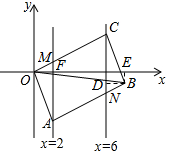 过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,直线x=6与AB交于点N,如图:
过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,直线x=6与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=6均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,$\left\{\begin{array}{l}{∠FOA=∠DBC}&{\;}\\{OA=BC}&{\;}\\{∠OAF=∠BCD}&{\;}\end{array}\right.$,
∴△OAF≌△BCD(ASA).
∴BD=OF=2,
∴OE=6+2=8,
∴OB=$\sqrt{O{E}^{2}+B{E}^{2}}$.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=8.
故答案为:8.
点评 本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
7.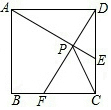 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3). 如图,在平行四边形ABCD中,对角线AC,BD相交于点O.
如图,在平行四边形ABCD中,对角线AC,BD相交于点O. 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题: