题目内容
 如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.(1)请问∠C与∠ABD是否相等,试说明理由;
(2)求证:AC∥DF.
考点:平行线的判定与性质
专题:常规题型
分析:(1)根据对顶角相等得∠2=∠4,加上∠1=∠2,利用等量代换得∠1=∠4,而∠1=∠3,所以∠3=∠4,根据平行线的判定得到BD∥CE,然后根据平行线的性质有∠C=∠ABD;
(2)由(1)得∠C=∠ABD,加上∠C=∠D,利用等量代换得∠D=∠ABD,然后根据平行线的判定方法即可得到AC∥DF.
(2)由(1)得∠C=∠ABD,加上∠C=∠D,利用等量代换得∠D=∠ABD,然后根据平行线的判定方法即可得到AC∥DF.
解答:解:(1)∠C与∠ABD相等.理由如下:
∵∠2=∠4,
而∠1=∠2,
∴∠1=∠4,
∵∠1=∠3,
∴∠3=∠4,
∴BD∥CE,
∴∠C=∠ABD;
(2)由(1)得∠C=∠ABD,
而∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
∵∠2=∠4,
而∠1=∠2,
∴∠1=∠4,
∵∠1=∠3,
∴∠3=∠4,
∴BD∥CE,
∴∠C=∠ABD;
(2)由(1)得∠C=∠ABD,
而∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
点评:本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
相关题目
已知a的平方根是±8,则a的立方根是( )
| A、2 | B、4 | C、±2 | D、±4 |
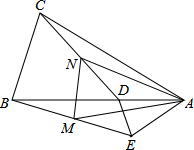 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论: 已知:如图,BC=BE,AB=FB,∠1=∠2,求证:∠C=∠BEF.
已知:如图,BC=BE,AB=FB,∠1=∠2,求证:∠C=∠BEF.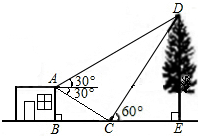 如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计).
如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计). 在平面直角坐标系中,已知A(2,0),B(3,1),C(1,3);
在平面直角坐标系中,已知A(2,0),B(3,1),C(1,3);