题目内容
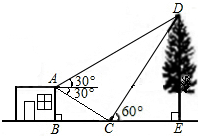 如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计).
如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:先在Rt△ABC中,由正弦函数的定义求出AC=8米,然后在Rt△ACD中,由正切函数的定义求出CD=8
米,最后解Rt△DCE,即可求出DE.
| 3 |
解答:解:由题意可知
∠ACB=30°,∠DAC=60°,∠ACD=90°,∠DCE=60°,
在Rt△ABC中,AC=
=
=8(米),
在Rt△ACD中,CD=AC•tan∠DAC=8×tan60°=8
(米),
在Rt△DCE中,DE=CD•sin∠DCE=8
×sin60°=12(米).
答:古树DE的高度为12米.
∠ACB=30°,∠DAC=60°,∠ACD=90°,∠DCE=60°,
在Rt△ABC中,AC=
| AB |
| sin∠ACB |
| 4 |
| sin30° |
在Rt△ACD中,CD=AC•tan∠DAC=8×tan60°=8
| 3 |
在Rt△DCE中,DE=CD•sin∠DCE=8
| 3 |
答:古树DE的高度为12米.
点评:本题考查了解直角三角形的应用,解题的关键是正确选择边角关系解直角三角形,难度一般.

练习册系列答案
相关题目
将抛物线y=3x2+c经过平移后,抛物线上的点(0,6)平移到点(2,9),那么平移后的抛物线的解析式为( )
| A、y=3(x-2)2+9 |
| B、y=3(x+2)2+9 |
| C、y=3x2+5 |
| D、y=3(x-2)2+6 |
 如图,AB为⊙O的直径,D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.
如图,AB为⊙O的直径,D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C. 如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D. 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=