题目内容
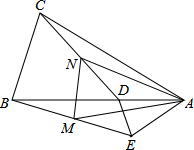 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论:(1)BE=CD;(2)D为AB的中点;(3)∠AMN=90°-
| ∠MAN |
| 2 |
其中正确的有
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:根据全等三角形的判定易证得△ACD≌△ABE,利用全等的性质有CD=BE,选项(1)正确;由M,N分别为BE,CD的中点,得到AN和AM为全等三角形△ACD、△ABE的对应中线,根据全等的性质得到AM=AN,即可判断△AMN为等腰三角形;根据等腰三角形的性质得∠AMN=∠ANM,由三角形的内角和定理得到∠AMN+∠ANM+∠MAN=180°,易得∠AMN=90°-
,选项(3)正确;选项(2)不一定成立.
| ∠MAN |
| 2 |
解答:解:在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴BE=CD,选项(1)正确;
D不一定为AB中点,选项(2)错误;
∵M,N分别为BE,CD的中点,即AN和AM为全等三角形△ACD、△ABE的对应边上的中线,
∴AM=AN,
∴∠AMN=∠ANM,
∵∠AMN+∠ANM+∠MAN=180°,
∴∠AMN=90°-
,选项(3)正确,
则正确的有(1),(3).
故答案为:(1),(3).
|
∴△ACD≌△ABE(SAS),
∴BE=CD,选项(1)正确;
D不一定为AB中点,选项(2)错误;
∵M,N分别为BE,CD的中点,即AN和AM为全等三角形△ACD、△ABE的对应边上的中线,
∴AM=AN,
∴∠AMN=∠ANM,
∵∠AMN+∠ANM+∠MAN=180°,
∴∠AMN=90°-
| ∠MAN |
| 2 |
则正确的有(1),(3).
故答案为:(1),(3).
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
3个连续偶数的和为36,则它们的积为( )
| A、1868 | B、1680 |
| C、1200 | D、998 |
 如图,已知平行四边形ABCD的面积是16,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是( )
如图,已知平行四边形ABCD的面积是16,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是( ) 如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.