题目内容
16．
如图，点A、B、C都在⊙O上，且BO=BC，则∠BAC=（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
分析 先根据BO=BC，OC=BO判断出△OBC的形状，再由圆周角定理即可得出结论．
解答 解：∵BO=BC，OC=BO，
∴△OBC是等边三角形，
∴∠BOC=60°，
∴∠BAC=$\frac{1}{2}$∠BOC=30°．
故选A．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
计算高手系列答案
相关题目
17．
如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为120m，则这栋楼的高度为（ ）
如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为120m，则这栋楼的高度为（ ）| A． | 160$\sqrt{3}$m | B． | 120$\sqrt{3}$m | C． | 300m | D． | 160$\sqrt{2}$m |
18．下列实数中，是无理数的为（ ）
| A． | -4 | B． | 0.101001 | C． | $\frac{1}{3}$ | D． | $\sqrt{2}$ |
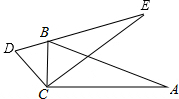如图：△ABC中，∠ACB=90°，∠A=20°，将△ABC绕点C逆时针方向旋转一个角度，到△DCE的位置，点B恰好在线段DE．那么旋转角∠BCD=40°．
11．
如图，点C在以AB为直径的⊙O上（点C不与A、B重合），点E在弦AC上，EF⊥AB于点F，若∠B=66°，则∠AEF的大小为（ ）
如图，点C在以AB为直径的⊙O上（点C不与A、B重合），点E在弦AC上，EF⊥AB于点F，若∠B=66°，则∠AEF的大小为（ ）| A． | 24° | B． | 33° | C． | 66° | D． | 76° |