题目内容
8.等腰三角形的三边长分别为10、10、12,则其内心与外心的距离为$\frac{5}{4}$.分析 过点A作AH⊥BC于H,根据角平分线的性质可得BH=CH,AH平分∠BAC,从而得到△ABC的外心O及内心I都在AH上.设△ABC外接圆的半径为R,内切圆的半径为r,连接IE、BI、OB,如图,在Rt△AHB中运用勾股定理可求出AH,在Rt△OHB中运用勾股定理可求出R,然后运用面积法可求出r,即可解决问题.
解答 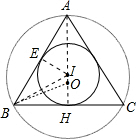 解:过点A作AH⊥BC于H,
解:过点A作AH⊥BC于H,
∵AB=AC,
∴BH=CH,AH平分∠BAC,
∴△ABC的外心O及内心I都在AH上.
设△ABC外接圆的半径为R,内切圆的半径为r,连接IE、BI、OB,如图,
在Rt△AHB中,
∵AB=10,BH=6,∴AH=8.
在Rt△OHB中,
OH2+BH2=OB2,
则(8-R)2+62=R2,
解得R=$\frac{25}{4}$,
∴OH=AH-AO=8-$\frac{25}{4}$=$\frac{7}{4}$.
∵S△ABH=S△ABI+S△BHI,
∴$\frac{1}{2}×6×8$=$\frac{1}{2}$×6r+$\frac{1}{2}$×10r,
解得r=3,
∴IH=3,
∴IO=IH-OH=3-$\frac{7}{4}$=$\frac{5}{4}$.
故答案为$\frac{5}{4}$.
点评 本题主要考查了三角形的内心和外心、等腰三角形的性质、圆的切线的性质、勾股定理等知识,在求三角形内切圆半径时巧妙地运用面积法,涉及到垂线段的长通常可考虑使用面积法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )
如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )
 如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )
如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
20.以下说法合理的是( )
| A. | 小明在10次抛图钉的试验中发现3次钉朝上,由此他说钉尖朝上的概率是30% | |
| B. | 抛掷一枚普通的正六面体骰子,出现6的概率是$\frac{1}{6}$的意思是每6次就有1次掷得6 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛掷硬币试验中,某同学估计硬币落地后,正面朝上的概率为$\frac{1}{2}$ |
 如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.
如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数. 如图,在平面直角坐标系中,有一个直角△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1A1C是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一个直角△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1A1C是由△ABC旋转得到的. 某市2012~2016年春节期间烟花爆竹销售量统计如图所示,根据统计图中提供的信息,预估2017年该市春节期间烟花爆竹销售量约为8万箱,你的预估理由是2012到2015年销售量下降明显,但2015到2015年下降趋势变缓.
某市2012~2016年春节期间烟花爆竹销售量统计如图所示,根据统计图中提供的信息,预估2017年该市春节期间烟花爆竹销售量约为8万箱,你的预估理由是2012到2015年销售量下降明显,但2015到2015年下降趋势变缓.