题目内容
4.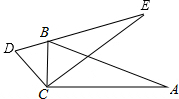 如图:△ABC中,∠ACB=90°,∠A=20°,将△ABC绕点C逆时针方向旋转一个角度,到△DCE的位置,点B恰好在线段DE.那么旋转角∠BCD=40°.
如图:△ABC中,∠ACB=90°,∠A=20°,将△ABC绕点C逆时针方向旋转一个角度,到△DCE的位置,点B恰好在线段DE.那么旋转角∠BCD=40°.
分析 首先由△ABC中,∠ACB=90°,∠A=20°,求得∠ABC的度数,然后由旋转的性质,求得△BCD为等腰三角形,且∠D=70°,继而求得答案.
解答 解:∵△ABC中,∠ACB=90°,∠A=20°,
∴∠ABC=90°-∠A=70°,
由旋转的性质可得:CB=CD,∠D=∠ABC=70°,
∴∠CBD=∠D=70°,
∴∠BCD=180°-∠D-∠CBD=40°.
故答案为:40°.
点评 此题考查了旋转的性质以及等腰三角形的性质.注意掌握旋转前后图形的对应关系是解此题的关键.

练习册系列答案
相关题目
16. 如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )
如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )
 如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )
如图,点A、B、C都在⊙O上,且BO=BC,则∠BAC=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
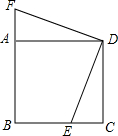 已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF.
已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF.
 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数. 某市2012~2016年春节期间烟花爆竹销售量统计如图所示,根据统计图中提供的信息,预估2017年该市春节期间烟花爆竹销售量约为8万箱,你的预估理由是2012到2015年销售量下降明显,但2015到2015年下降趋势变缓.
某市2012~2016年春节期间烟花爆竹销售量统计如图所示,根据统计图中提供的信息,预估2017年该市春节期间烟花爆竹销售量约为8万箱,你的预估理由是2012到2015年销售量下降明显,但2015到2015年下降趋势变缓.