题目内容

17．如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为120m，则这栋楼的高度为（　　）
A．160$\sqrt{3}$mB．120$\sqrt{3}$mC．300mD．160$\sqrt{2}$m

分析 首先过点A作AD⊥BC于点D，根据题意得∠BAD=30°，∠CAD=60°，AD=120m，然后利用三角函数求解即可求得答案．

解答 解：过点A作AD⊥BC于点D，则∠BAD=30°，∠CAD=60°，AD=120m，
在Rt△ABD中，BD=AD•tan30°=120×$\frac{\sqrt{3}}{3}$=40$\sqrt{3}$（m），
在Rt△ACD中，CD=AD•tan60°=120×$\sqrt{3}$=120$\sqrt{3}$（m），
∴BC=BD+CD=160$\sqrt{3}$（m）．
故选A．

点评 此题考查了仰角俯角问题．注意准确构造直角三角形是解此题的关键．

练习册系列答案
相关题目
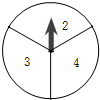7．商场为了促销某件商品，设置了如图的一个转盘，它被分成了3个相同的扇形．各扇形分别标有数字2，3，4，指针的位置固定，该商品的价格由顾客自由转动此转盘两次来获取，每次转动后让其自由停止，记下指针所指的数字（指针指向两个扇形的交线时，当作右边的扇形），先记的数字作为价格的十位数字，后记的数字作为价格的个位数字，则顾客购买商品的价格不超过30元的概率是多少？
8．如果一条抛物线y=ax2+bx+c（a≠0）与x轴的两个交点为A，B（点A在点B的左侧），顶点为P，连接PA，PB，那么称△PAB为这条抛物线的“抛物线三角形”．
（1）请写出“抛物线三角形”是等腰直角三角形时，抛物线的表达式（写出一个即可）y=-x2+1；
（2）若抛物线y=-x2+bx（b＞0）的“抛物线三角形”是等边三角形，求b的值；
（3）若△PAB是抛物线y=-x2+c的“抛物线三角形”，是否存在以点A为对称中心的矩形PBCD？若存在，求出过O，C，D三点的抛物线的表达式；若不存在，说明理由．
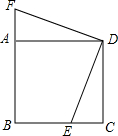5．已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．
12．如图，点A（m，4），B（-4，n）在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，经过点A、B的直线与x轴相交于点C，与y轴相交于点D．
（1）若m=2，求n的值；
（2）求m+n的值；
（3）连接OA、OB，若tan∠AOD+tan∠BOC=1，求直线AB的函数关系式．
2．如图，四边形ABCD内接于⊙O，对角线AC为⊙O的直径，过点C作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF．
（1）求∠CDE的度数；
（2）求证：DF是⊙O的切线；
（3）若AC=2$\sqrt{5}$DE，求tan∠ABD的值．
9．如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为24．
6．2016年《政府工作报告》中提出了十大新词汇，为了解同学们对新词汇的关注度，某数学兴趣小组选取其中的A：“互联网+政务服务”，B：“工匠精神”，C：“光网城市”，D：“大众旅游时代”四个热词在全校学生中进行了抽样调查，要求被调查的每位同学只能从中选择一个我最关注的热词．根据调查结果，该小组绘制了如下的两幅不完整的统计图．

请你根据统计图提供的信息，解答下列问题：
（1）本次调查中，一共调查了多少名同学？
（2）条形统计图中，m=60，n=90；
（3）扇形统计图中，热词B所在扇形的圆心角是多少度？
16．如图，点A、B、C都在⊙O上，且BO=BC，则∠BAC=（　　）
A．30°B．40°C．50°D．60°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网