题目内容
15．如图（1），B是线段AD上一点，分别以AB、BD为边在AD同侧作等边△ABC和等边△BDE，得到（1）△ABE≌△CBD；（2）AE与CD相交所得的锐角为60°．如图（2），B是线段AE上一点，分别以AB、BE为边在AE同侧作正方形ABCD和正方形BEFG，除了得到△ABG≌△CBE外，AG与CE相交所得的角的度数为（ ）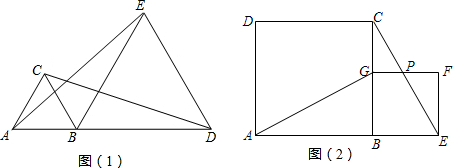
| A． | 90° | B． | 60° | C． | 120° | D． | 不能确定 |
分析 延长EC交AG于M，由全等三角形的性质得出∠G=∠E，由角的互余关系和对顶角相等得出∠G+∠GCM=90°，因此∠GMC=90°，即可得出结论．
解答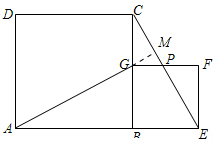 
解：延长EC交AG于M，如图所示：
∵△ABG≌△CBE，
∴∠G=∠E，
∵∠E+∠BCE=90°，∠GCM=∠BCE，
∴∠G+∠GCM=90°，
∴∠GMC=90°，
∴AG⊥EC．
∴AG与CE相交所得的角的度数为90°．
故选：A．
点评 本题考查了全等三角形的判定与性质、正方形的性质、对顶角相等；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．
练习册系列答案
相关题目
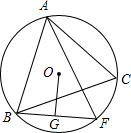已知△ABC内接于⊙O，F是弧$\widehat{BC}$上一点，OG⊥BF于点G，且OG=$\frac{1}{2}$AC．证明：AF⊥BC．
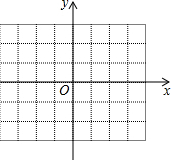如图是一个平面直角坐标系，在坐标系中描出下列各点：A（1，2），B（3，2），C（-1，1），D（-1，-2）．