题目内容
12.桌子上放着背面而完全相同的3张扑克牌,分别为2张红桃和1张黑桃,现从中任意取出一张扑克牌,记下扑克牌花色,再从剩余的扑克牌中任意取出一张扑克牌,记下扑克牌的花色,求两次记下的花色不同的概率(请用“画树状图”或“列表”等方法,写出分析过程,并给出结果)分析 通过列表将所有等可能的结果列举出来,利用概率公式求解即可.
解答 解:(1)列表得:
| 红 | 红 | 黑 | |
| 红 | 相同 | 不同 | |
| 红 | 相同 | ||
| 黑 | 不同 | 不同 | 相同 |
∴两次记下的花色不同的概率为$\frac{4}{6}$=$\frac{2}{3}$.
点评 本题考查了列表法与树状图法,解题的关键是通过列表或树形图能够将所有等可能的结果全部列举出来,难度不.

练习册系列答案
相关题目
20.如果一个多边形的内角和等于1260°,那么这个多边形的边数为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
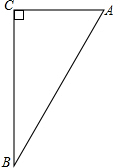 如图,在△ABC中,∠C=90°.
如图,在△ABC中,∠C=90°. 如图,在△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数.
如图,在△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数.