Question

4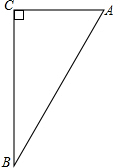．如图，在△ABC中，∠C=90°．
（1）若BC=5，AB=6，求AC的长
（2）若∠B=30°，BC=3，求AC的长．

Answer 1

分析 （1）直接利用勾股定理求得答案即可；
（2）由∠C=90°，∠B=30°，得出AB=2AC，设AC为x，利用勾股定理列出方程求得答案即可．

解答 解：（1）AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{11}$；
（2）∵∠C=90°，∠B=30°，
∴AB=2AC，
设AC为x，
由勾股定理得
x²+3²=（2x）²
解得：x=$\sqrt{3}$
即AC=$\sqrt{3}$．

点评 此题考查勾股定理的运用，含30°直角三角形的性质，掌握勾股定理是解决问题的关键．