题目内容
2.在$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,…$\sqrt{2013}$,$\sqrt{2014}$中,无理数的个数有1970个.分析 根据$\sqrt{4{4}^{2}}$$<\sqrt{2014}$<$\sqrt{4{5}^{2}}$,可得有理数的个数,根据无理数是无限不循环小数,可得答案.
解答 解:由$\sqrt{4{4}^{2}}$$<\sqrt{2014}$<$\sqrt{4{5}^{2}}$,得$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,…$\sqrt{2013}$,$\sqrt{2014}$中,有理数有44个,
无理数有2014-44=1970(个).
故答案为:1970.
点评 本题考查了无理数,利用$\sqrt{4{4}^{2}}$$<\sqrt{2014}$<$\sqrt{4{5}^{2}}$得出有理数的个数是解题关键.

练习册系列答案
相关题目
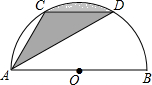 如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.
如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.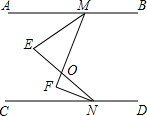 如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于O点
如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于O点 如图,利用一面墙(墙的长度不限),另三边用20m长的篱笆围成一个积为50m2的矩形场地,求矩形的长和宽各是多少.
如图,利用一面墙(墙的长度不限),另三边用20m长的篱笆围成一个积为50m2的矩形场地,求矩形的长和宽各是多少.