Question

18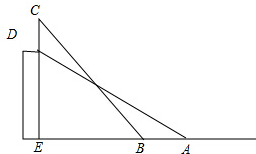．如图所示，某高校的教学大楼上竖有一根避雷针CD，小明为了知道避雷针CD的长度，在点A测得点D的仰角为30°，小明向大楼方向行进16m到达点B，又测得点C的仰角为45°，若大楼DE高度为24m，求避雷针CD的长度（结果保留根号）．

Answer 1

分析 根据三角函数的定义得到AE=$\frac{3DE}{\sqrt{3}}$=24$\sqrt{3}$m，于是得到BE=AE-AB=（24$\sqrt{3}$-16）m，根据三角函数的定义得到CE=BE=（24$\sqrt{3}$-16）m，于是得到结论．

解答 解：由题意得DE=24m，AB=16m，∠A=30°，∠CBE=45°，
在Rt△ADE中，tan∠A=tan30°=$\frac{\sqrt{3}}{3}$=$\frac{DE}{AE}$，
∴AE=$\frac{3DE}{\sqrt{3}}$=24$\sqrt{3}$m，
∴BE=AE-AB=（24$\sqrt{3}$-16）m，
∵tan∠CBE=tan45°=1=$\frac{CE}{BE}$，
∴CE=BE=（24$\sqrt{3}$-16）m，
∴CD=CE-DE=24$\sqrt{3}$-16-24=（24$\sqrt{3}$-40）m．
答：避雷针CD的长度（2$\sqrt{3}$-40）m．

点评 本题考查了解直角三角形的应用，利用锐角三角函数的知识求出线段CE和DE的长，从而根据CD=CE-DE得出问题的答案是解决本题的关键．