题目内容
18.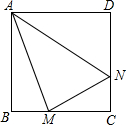 如图,正方形ABCD的边长为6cm.点M为BC上一点(点M不与B,C重合)点N为CD上一点,∠MAN=45°.
如图,正方形ABCD的边长为6cm.点M为BC上一点(点M不与B,C重合)点N为CD上一点,∠MAN=45°.(1)求证:BM+DN=MN;
(2)设BM=x,DN=y,写出y关于x的函数关系式,并指出自变量x的取值范围.
分析 (1)延长CB到Q使BQ=DN,连接AQ,根据SAS证△DAN≌△BAQ,求出AN=AQ,∠DAN=∠BAQ,求出∠NAM=∠MOQ=45°,根据SAS证△NAM≌△QAM,推出DN+BM=MN,根据三角形的周长得出△CNM的周长等于DC+BC,代入求出即可.
(2)根据(1)的结论,根据勾股定理列出x、y的等式,整理变形后即可求得.
解答 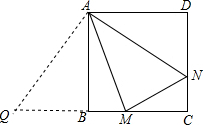 解:(1)延长CB到Q,使BQ=DN,连接AQ,
解:(1)延长CB到Q,使BQ=DN,连接AQ,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠DAB=∠ABC=∠ABQ=90°,
在△ADN和△ABQ中,
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABQ}\\{DN=BQ}\end{array}\right.$,
∴△ADN≌△ABQ(SAS),
∴∠DAN=∠BAQ,AN=AQ,
∵∠DAB=90°,∠MAN=45°,
∴∠DAN+∠BAM=45°,
∴∠BAM+∠QAB=45°,
即∠MAN=∠MAQ,
在△MAN和△MAQ中,
$\left\{\begin{array}{l}{AN-=AQ}\\{∠NAM=∠MAQ}\\{AM=AM}\end{array}\right.$,
∴△MAN≌△MAQ,
∴MN=MQ=BM+DN,
即BM+DN=MN.
(2)设BM=x,DN=y,
∵正方形ABCD的边长为6cm.
∴CM=6-x,CN=6-y,
∵MN=x+y,
根据勾股定理得出(x+y)2=(6-x)2+(6-y)2,
整理得,xy=36-6x-6y,
∴y=$\frac{36-6x}{6+x}$(0<x<6).
点评 本题考查了正方形性质,全等三角形的性质和判定的应用,关键是考查学生的推理能力,题目具有一定的代表性,是一道综合性比较强的题目,有一定的难度.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 一组对边相等且平行的四边形是平行四边形 | |
| B. | 有两边相等的四边形是平行四边形 | |
| C. | 四个全等的三角形一定可组成一个平行四边形 | |
| D. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
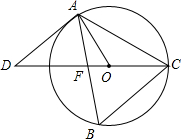 如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.
如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.