题目内容
6.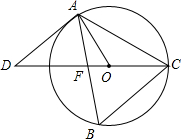 如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.
如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.(1)说明:DA是⊙O的切线;
(2)若AB=AC,AB交CE于点F,且EF=4,ED=3,求AF的长.
分析 (1)根据圆周角定理求出∠AOC=132°,进而求得∠AOD=48°,即可求得∠AOD+∠D=90°,证得OA⊥AD,从而得出结论;
(2)连接AE,根据切线的性质圆周角定理和等腰三角形的性质得出∠DAF=∠AEF,即可证得△AFE∽△DFA,根据相似三角形的性质即可求得AF.
解答 (1)证明:∵∠B=66°,
∴∠AOC=2∠B=132°,
∴∠AOD=48°,
∵∠D=42°,
∴∠AOD+∠D=90°,
∴OA⊥AD,
∴DA是⊙O的切线;
(2)解:连接AE,如图,
∵AB=AC,
∴∠B=∠ACB,
∵DA是⊙O的切线,
∴∠DAF=∠ACB,
∴∠DAF=∠B,
∵∠B=∠AEF,
∴∠DAF=∠AEF,
∵∠AFE=∠DFA,
∴△AFE∽△DFA,
∴$\frac{EF}{AF}$=$\frac{AF}{DF}$,
∵EF=4,ED=3,
∵DF=7,
∴$\frac{4}{AF}$=$\frac{AF}{7}$,
∴AF=2$\sqrt{7}$.
点评 本题考查了切线的判定、等腰三角形的性质、圆周角定理以及三角形相似的判定,解答本题的关键是掌握切线的判定定理、圆周角定理以及三角形相似的判定.

练习册系列答案
相关题目
17.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b、k的值分别为( )
| A. | 0 5 | B. | 0 1 | C. | -4 5 | D. | -4 1 |
1.如果α是锐角,则下列成立的是( )
| A. | sinα+cosα=1 | B. | sinα+cosα>1 | C. | sinα+cosα<1 | D. | sinα+cosα≤1 |
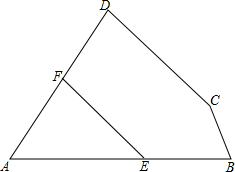 如图,E,F是四边形ABCD的边AB,AD上的两点,若∠B+∠C+∠D-∠BEF-∠DFE=60°,求∠A的度数.
如图,E,F是四边形ABCD的边AB,AD上的两点,若∠B+∠C+∠D-∠BEF-∠DFE=60°,求∠A的度数.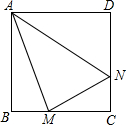 如图,正方形ABCD的边长为6cm.点M为BC上一点(点M不与B,C重合)点N为CD上一点,∠MAN=45°.
如图,正方形ABCD的边长为6cm.点M为BC上一点(点M不与B,C重合)点N为CD上一点,∠MAN=45°.