题目内容
7.已知|2a-b+1|+(3a+$\frac{3}{2}$b)2=0,求代数式$\frac{{b}^{2}}{a+b}$÷($\frac{a}{a-b}$-1)•(a-$\frac{{a}^{2}}{a-b}$)的值.分析 根据非负数的性质列出方程组求出a,b,再根据分式的混合运算法则先化简后代入即可.
解答 解:∵|2a-b+1|+(3a+$\frac{3}{2}$b)2=0,
又∵|2a-b+1|≥0,(3a+$\frac{3}{2}$b)2≥0,
∴$\left\{\begin{array}{l}{2a-b=-1}\\{3a=-\frac{3}{2}b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴原式=$\frac{{b}^{2}}{a+b}$÷($\frac{a-a+b}{a-b}$)•$\frac{{a}^{2}-ab-{a}^{2}}{a-b}$
=$\frac{{b}^{2}}{a+b}$•$\frac{a-b}{b}$•$\frac{-ab}{a-b}$
=-$\frac{a{b}^{2}}{a+b}$
=-$\frac{-\frac{1}{4}×\frac{1}{4}}{-\frac{1}{4}+\frac{1}{2}}$
=$\frac{1}{4}$.
点评 本题考查非负数的性质、分式的混合运算、解方程组等知识,正确运用法则是解题的关键,是中考常考题型,可以通过此类题目的训练提高计算能力.

练习册系列答案
相关题目
17.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b、k的值分别为( )
| A. | 0 5 | B. | 0 1 | C. | -4 5 | D. | -4 1 |
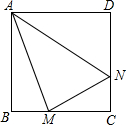 如图,正方形ABCD的边长为6cm.点M为BC上一点(点M不与B,C重合)点N为CD上一点,∠MAN=45°.
如图,正方形ABCD的边长为6cm.点M为BC上一点(点M不与B,C重合)点N为CD上一点,∠MAN=45°.