��Ŀ����
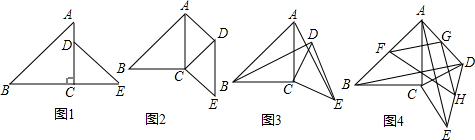
7����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=a��x-h��2+k�Ķ���A������Ϊ��1��0������y�ύ��B������Ϊ��0��$\frac{\sqrt{3}}{2}$������1���������ߵĽ���ʽ������ʽ���ɣ���
��2����ͼ2��ֱ��y=$\frac{\sqrt{3}}{3}$x+b��x�ύ�ڵ�C����y�ύ�ڵ�D������A����ֱ��CD�ĶԳƵ�Eǡ�������������ϣ���E�����ꣻ
��3���ڣ�2���������£�P�ǶԳ����Ҳ���������һ�㣬����P��x���ƽ���߽��߶�CD�ڵ�Q������PE��QE����P�������Ϊt������PEQ=60��ʱ����t��ֵ��

���� ��1���ȸ��ݶ����������h��k���ٰѵ㣨0��$\frac{\sqrt{3}}{2}$�����뼴�����a��
��2��������ֱ�ߴ�ֱk�ij˻�Ϊ-1�������ֱ��AE�����÷����鼴�������E���꣮
��3����֤��E��Q��A��P�ĵ㹲Բ���õ���QAP=120�㣬��֤����ADQ�ס�AMP����$\frac{DQ}{PM}$=$\frac{AD}{AM}$���г����̼��ɽ�����⣮
��� �⣺��1����������y=a��x-h��2+k�Ķ���A������Ϊ��1��0����
��h=1��k=0��
�������߽���ʽΪy=a��x-1��2��
�ѵ㣨0��$\frac{\sqrt{3}}{2}$������õ�a=$\frac{\sqrt{3}}{2}$��
�������ߵĽ���ʽΪy=$\frac{\sqrt{3}}{2}$��x-1��2��
��2����ͼ���ߵ�A����ֱ��CD�ĶԳƵ�Eǡ�������������ϣ�
��AE��CD��
��ֱ��CD����ʽΪy=$\frac{\sqrt{3}}{3}$x+b��
����Լ���ֱ��AE�Ľ���ʽΪy=-$\sqrt{3}$x+b���ѵ㣨1��0�������b=$\sqrt{3}$��
��ֱ��AE����ʽΪy=-$\sqrt{3}$x+$\sqrt{3}$��
��$\left\{\begin{array}{l}{y=-\sqrt{3}x+\sqrt{3}}\\{y=\frac{\sqrt{3}}{2}��x-1��^{2}}\end{array}\right.$���$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$���ᣩ��$\left\{\begin{array}{l}{x=-1}\\{y=2\sqrt{3}}\end{array}\right.$��
���E������-1.2$\sqrt{3}$����
��3����ͼ��PE��CD���ӳ��߽��ڵ�N����PM��OA��M�����P����[t��$\frac{\sqrt{3}}{2}$��t-1��2]
�ɣ�2����֪��E��-1��2$\sqrt{3}$����A��1��0����
��AE���е����꣨0��$\sqrt{3}$�����ѣ�0��$\sqrt{3}$������y=$\frac{\sqrt{3}}{3}$x+b�õ�b=$\sqrt{3}$��
���D���꣨0��$\sqrt{3}$����
���D��AE�е㣮DE=DA��
��CD��ֱƽ��AE��
��NE=NA��QE=QA��
���1=��2����QEA=��QAE��
���PEQ=��QAN=60�㣬
��tan��DCO=$\frac{OD}{CO}$=$\frac{\sqrt{3}}{3}$��
���DCO=30�㣬
���CAD=60�㣬
���CAD=��QAN��
���4=��2��
��PQ��CA��
���3=��4��
���1=��3��
��E��Q��A��P�ĵ㹲Բ��
���QAP+��PEQ=180�㣬
���QAP=120�㣬
�ߡ�4+��PAM=60�㣬��4+��QAD=60�㣬
���PAM=��QAD���ߡ�ADQ=��PMA=90�㣬
���ADQ�ס�AMP��
��$\frac{DQ}{PM}$=$\frac{AD}{AM}$��
��$\frac{2\sqrt{3}-\sqrt{3}��t-1��^{2}}{\frac{\sqrt{3}}{2}��t-1��^{2}}$=$\frac{2}{t-1}$��
���t=2��-1����������
��t=2��
���� ���⿼����κ����ۺ��⡢��ԳƵ����ʡ�һ�κ������ĵ㹲Բ�����������ε��ж������ʵ�֪ʶ������Ĺؼ����������մ���ϵ����ȷ����������ʽ�������������У�֤���ĵ㹲Բ�ǽ����ͻ�ƿڣ����������������ε������г����̽�����⣬�����п�ѹ���⣮

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�| A�� | 1��2��2��1 | B�� | 2��1��1��1 | C�� | 1��2��3��4 | D�� | 2��1��2��1 |
| A�� | 4��6��8 | B�� | 4��8��10 | C�� | 6��8��10 | D�� | 8��10��12 |
 �����龳��
�����龳��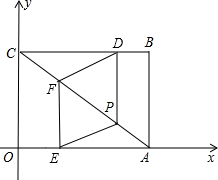 ��ֱ������ϵ�У���OΪԭ�㣬��B������Ϊ��4��3�����ı���ABCO�Ǿ��Σ���D��B������ÿ��1����λ���ٶ����յ�C�˶���ͬʱ��E��O�������ÿ��1����λ���ٶ����յ�A�˶�����D��DP��BC��AC���ڵ�P����E��EF��AO��AC���ڵ�F������DF��PE��
��ֱ������ϵ�У���OΪԭ�㣬��B������Ϊ��4��3�����ı���ABCO�Ǿ��Σ���D��B������ÿ��1����λ���ٶ����յ�C�˶���ͬʱ��E��O�������ÿ��1����λ���ٶ����յ�A�˶�����D��DP��BC��AC���ڵ�P����E��EF��AO��AC���ڵ�F������DF��PE�� ��ͼ��һ�κ���y=$\frac{1}{2}$x+2��ͼ����x�ύ�ڵ�B���뷴��������y=$\frac{k}{x}$��k��0����ͼ���һ������ΪA��2��m����
��ͼ��һ�κ���y=$\frac{1}{2}$x+2��ͼ����x�ύ�ڵ�B���뷴��������y=$\frac{k}{x}$��k��0����ͼ���һ������ΪA��2��m���� ��1����ʽ��$\left\{\begin{array}{l}{x+3��\frac{1}{2}x}\\{5-2x��9}\end{array}\right.$�Ľ⼯��
��1����ʽ��$\left\{\begin{array}{l}{x+3��\frac{1}{2}x}\\{5-2x��9}\end{array}\right.$�Ľ⼯�� ��ͼ����ֱ������ϵ�У��ı���OABC�Ķ���O��A��C������ֱ��ǣ�0��0������5��0������2��3��������B������Ϊ��7��3��ʱ���ı���OABC��ƽ���ı��Σ�
��ͼ����ֱ������ϵ�У��ı���OABC�Ķ���O��A��C������ֱ��ǣ�0��0������5��0������2��3��������B������Ϊ��7��3��ʱ���ı���OABC��ƽ���ı��Σ�