题目内容
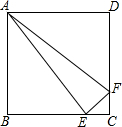 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.考点:函数关系式
专题:
分析:△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,分别表示正方形ABCD的面积、△ABE的面积、△ADF的面积、△ECF的面积代入即可.
解答:解:设运动时间为x(s),
∵点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,
∴CE=2x,CF=2x,BE=4-2x,DF=4-2x,
∴△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,
即:y=16-
•AB•BE-
•AD•DF-
•EC•FC
=16-
•4•(4-2x)-
•4•(4-2x)-
•2x•2x
=-2x2+8x.(0≤x≤2)
∵点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,
∴CE=2x,CF=2x,BE=4-2x,DF=4-2x,
∴△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,
即:y=16-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=16-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-2x2+8x.(0≤x≤2)
点评:此题考查了函数关系式,解题关键是正确表示正方形ABCD的面积、△ABE的面积、△ADF的面积、△ECF的面积.

练习册系列答案
相关题目
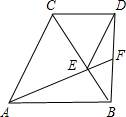 如图,△ABC和△CDE都为等边三角形,E在BC上,AE的延长线交BD于F.
如图,△ABC和△CDE都为等边三角形,E在BC上,AE的延长线交BD于F.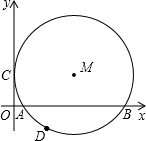 如图,⊙M与y轴相切于点C,与x轴交于A(2-
如图,⊙M与y轴相切于点C,与x轴交于A(2-
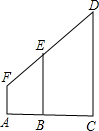 如图,EB=5,AB=4,AC=12,AF=1.6,求CD的长.
如图,EB=5,AB=4,AC=12,AF=1.6,求CD的长. 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为
如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为