题目内容
若一个n边形的边数增加一倍,则内角和将增加 .
考点:多边形内角与外角
专题:
分析:n边形的内角和是(n-2)•180°,将n边形的边数增加一倍就变成2n边形,2n边形的内角和是(2n-2)•180°,据此即可求得增加的度数.
解答:解:∵n边形的内角和是(n-2)•180°,
∴2n边形的内角和是(2n-2)•180°,
∴将n边形的边数增加一倍,则它的内角和增加:(2n-2)•180°-(n-2)•180°=n×180°.
故答案为n×180°.
∴2n边形的内角和是(2n-2)•180°,
∴将n边形的边数增加一倍,则它的内角和增加:(2n-2)•180°-(n-2)•180°=n×180°.
故答案为n×180°.
点评:本题主要考查了多边形的内角和公式,整式的化简,都是需要熟练掌握的内容.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
把一个边长为3cm的正方形的各边长都增加x cm,则正方形增加的面积y(cm2)与x(cm)之间的函数表达式是( )
| A、y=(x+3)2 |
| B、y=x2+6x+6 |
| C、y=x2+6x |
| D、y=x2 |
若等腰三角形的周长为60cm,底边长为x cm,一腰长为y cm,则y与x的函数关系式及自变量x的取值范围是( )
| A、y=60-2x(0<x<60) | ||
| B、y=60-2x(0<x<30) | ||
C、y=
| ||
D、y=
|
已知反比例函数y=
的图象经过点(1,-2),则k的值为( )
| k |
| 2x |
| A、1 | B、-4 | C、-1 | D、4 |
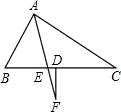 如图,AF平分∠BAC,FD⊥BD.
如图,AF平分∠BAC,FD⊥BD.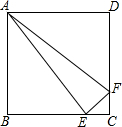 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.