题目内容
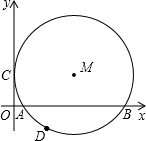 如图,⊙M与y轴相切于点C,与x轴交于A(2-
如图,⊙M与y轴相切于点C,与x轴交于A(2-| 3 |
| 3 |
 |
| AD |
| 1 |
| 2 |
 |
| BD |
(1)求⊙M的半径;
(2)P是⊙M上一个动点,若以P、A、D、B为顶点的四边形是梯形,求∠PAD的度数;
(3)如图2,点Q是⊙M上一个动点,点N为OQ的中点,连接CN,当点Q在⊙M上运动时,CN的最大值为多少?
考点:圆的综合题
专题:综合题
分析:(1)如图1,作ME⊥x轴于E,连接MC,根据垂径定理,由ME⊥AB得AE=BE=
,则OE=OA+AE=2,再根据切线的性质得到MC⊥y轴,所以四边形MEOC为矩形,于是得到MC=OE=2;
(2)连接MA、MB,MD,如图1,在Rt△MAE中利用勾股定理计算出ME=1,根据含30度的直角三角形三边的关系得到∠MAE=30°,则∠AMB=120°,由于
=
,根据圆周角定理
得∠AMD=
∠AMB=40°,然后分类讨论:当PD∥BA时,如图1①,根据平行线的性质与圆周角定理可得∠PAD=20°;当PA∥BD时,如图1②,∠PAD=60°;当PB∥AD时,如图1③,∠PAD=120°;
(3)连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,先根据勾股定理计算出OM=
,根据直角三角形斜边上的中线性质得CK=
,易得NK为△OQM的中位线,则NK=
QM=1,
根据三角形三边的关系得到,当∠CKN=180°时,CN最大,此时CN=CK+NK=
+1.
| 3 |
(2)连接MA、MB,MD,如图1,在Rt△MAE中利用勾股定理计算出ME=1,根据含30度的直角三角形三边的关系得到∠MAE=30°,则∠AMB=120°,由于
 |
| AD |
| 1 |
| 2 |
 |
| BD |
得∠AMD=
| 1 |
| 3 |
(3)连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,先根据勾股定理计算出OM=
| 5 |
| ||
| 2 |
| 1 |
| 2 |
根据三角形三边的关系得到,当∠CKN=180°时,CN最大,此时CN=CK+NK=
| ||
| 2 |
解答: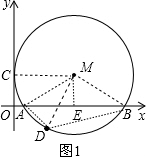 解:(1)如图1,作ME⊥x轴于E,连接MC,
解:(1)如图1,作ME⊥x轴于E,连接MC,
∵A(2-
,0)、点B(2+
,0),
∴AB=2
,
∵ME⊥AB,
∴AE=BE=
,
∴OE=OA+AE=2-
+
=2,
∵⊙M与y轴相切于点C,
∴MC⊥y轴,
∴四边形MEOC为矩形,
∴MC=OE=2,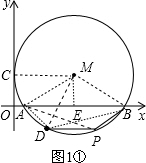
即⊙M的半径为2;
(2)连接MA、MB,MD,如图1,
在Rt△MAE中,∵AE=
,MA=2,
∴ME=
=1,
∴∠MAE=30°,
∴∠AMB=120°,
∵
=
,
∴∠AMD=
∠AMB=40°,
当PD∥BA时,如图1①,
则∠BAP=∠APD,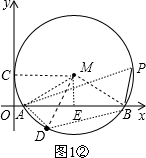
∴
=
,
而
=
,
∴
=
,
∴∠PAD=
∠AMD=20°;
当PA∥BD时,如图1②,
∵∠APB=
∠AMB=60°,
∴∠ADB=180°-∠APB=120°,
∵PA∥BD,
∴∠PAD=180°-∠ADB=60°;
当PB∥AD时,如图1③,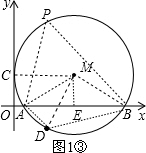
∵PB∥AD,
∴∠PAD+∠APB=180°,
∵∠APB=
∠AMB=60°,
∴∠PAD=120°;
(3)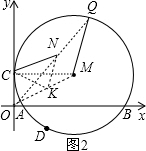 连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,
连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,
∵OC=1,MC=2,
∴OM=
=
,
∴CK=
,
∵N点为OQ的中点,
∴NK为△OQM的中位线,
∴NK=
QM=1,
∵点Q是⊙M上一个动点,
∴当∠CKN=180°时,CN最大,此时CN=CK+NK=
+1,
即CN的最大值为
+1.
 解:(1)如图1,作ME⊥x轴于E,连接MC,
解:(1)如图1,作ME⊥x轴于E,连接MC,∵A(2-
| 3 |
| 3 |
∴AB=2
| 3 |
∵ME⊥AB,
∴AE=BE=
| 3 |
∴OE=OA+AE=2-
| 3 |
| 3 |
∵⊙M与y轴相切于点C,
∴MC⊥y轴,
∴四边形MEOC为矩形,
∴MC=OE=2,

即⊙M的半径为2;
(2)连接MA、MB,MD,如图1,
在Rt△MAE中,∵AE=
| 3 |
∴ME=
| MA2-AE2 |
∴∠MAE=30°,
∴∠AMB=120°,
∵
 |
| AD |
| 1 |
| 2 |
 |
| BD |
∴∠AMD=
| 1 |
| 3 |
当PD∥BA时,如图1①,
则∠BAP=∠APD,

∴
 |
| AD |
 |
| BP |
而
 |
| AD |
| 1 |
| 2 |
 |
| BD |
∴
 |
| AD |
 |
| DP |
∴∠PAD=
| 1 |
| 2 |
当PA∥BD时,如图1②,
∵∠APB=
| 1 |
| 2 |
∴∠ADB=180°-∠APB=120°,
∵PA∥BD,
∴∠PAD=180°-∠ADB=60°;
当PB∥AD时,如图1③,

∵PB∥AD,
∴∠PAD+∠APB=180°,
∵∠APB=
| 1 |
| 2 |
∴∠PAD=120°;
(3)
 连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,
连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,∵OC=1,MC=2,
∴OM=
| 12+22 |
| 5 |
∴CK=
| ||
| 2 |
∵N点为OQ的中点,
∴NK为△OQM的中位线,
∴NK=
| 1 |
| 2 |
∵点Q是⊙M上一个动点,
∴当∠CKN=180°时,CN最大,此时CN=CK+NK=
| ||
| 2 |
即CN的最大值为
| ||
| 2 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和切线的性质;会利用勾股定理计算线段的长;理解坐标与图形的性质;会运用分类讨论的思想解决数学问题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若等腰三角形的周长为60cm,底边长为x cm,一腰长为y cm,则y与x的函数关系式及自变量x的取值范围是( )
| A、y=60-2x(0<x<60) | ||
| B、y=60-2x(0<x<30) | ||
C、y=
| ||
D、y=
|
 如图,已知△ABC和△ECD都是直角等腰三角形,∠ACB=∠DCE=90°,若∠ACD=30°,求∠AED的度数.
如图,已知△ABC和△ECD都是直角等腰三角形,∠ACB=∠DCE=90°,若∠ACD=30°,求∠AED的度数. 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.
如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.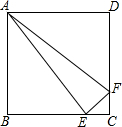 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围. 如图所示,分别求出扇形丙、丁的圆心角及甲、乙的面积比.
如图所示,分别求出扇形丙、丁的圆心角及甲、乙的面积比.