题目内容
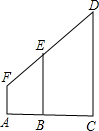 如图,EB=5,AB=4,AC=12,AF=1.6,求CD的长.
如图,EB=5,AB=4,AC=12,AF=1.6,求CD的长.考点:相似三角形的判定与性质
专题:
分析:延长CA,DF交于点G,易证△GAF∽△GBE,可求得GA的值,根据△GAF∽△GCD即可求得CD的值.
解答:解:延长CA,DF交于点G,

∵AF∥BE,
∴△GAF∽△GBE,
∴
=
=
,
解得:GA=
,
∵△GAF∽△GCD,
∴
=
,
∴CD=
.

∵AF∥BE,
∴△GAF∽△GBE,
∴
| FA |
| BE |
| GA |
| GB |
| GA |
| GA+AB |
解得:GA=
| 32 |
| 17 |
∵△GAF∽△GCD,
∴
| GA |
| GC |
| AF |
| CD |
∴CD=
| 23 |
| 2 |
点评:本题考查了相似三角形的判定考查了相似三角形对应边比例相等的性质.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
把一个边长为3cm的正方形的各边长都增加x cm,则正方形增加的面积y(cm2)与x(cm)之间的函数表达式是( )
| A、y=(x+3)2 |
| B、y=x2+6x+6 |
| C、y=x2+6x |
| D、y=x2 |
若等腰三角形的周长为60cm,底边长为x cm,一腰长为y cm,则y与x的函数关系式及自变量x的取值范围是( )
| A、y=60-2x(0<x<60) | ||
| B、y=60-2x(0<x<30) | ||
C、y=
| ||
D、y=
|
若二次函数y=-(x-a)2+a-1的顶点在第四象限,则a的取值范围为( )
| A、a>1 | B、a<0 |
| C、0<a<1 | D、无法确定 |
 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.
如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.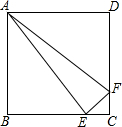 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围. 如图所示,分别求出扇形丙、丁的圆心角及甲、乙的面积比.
如图所示,分别求出扇形丙、丁的圆心角及甲、乙的面积比.