题目内容
在平面直角坐标系中,O为坐标原点,直线y=x+1与⊙O相切,则圆O的半径为 .
考点:切线的性质,一次函数图象上点的坐标特征
专题:计算题
分析:如图,直线y=x+1与x轴交于点B,与y轴交于点A,作OC⊥AB于C,先根据坐标轴上点的坐标特征得到A(0,1),B(-1,0),则可判断△OAB为等腰直角三角形,所以AB=
OA=
,OC=
AB=
,然后根据切线的性质即可得到圆O的半径为
.
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:解: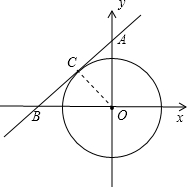 如图,直线y=x+1与x轴交于点B,与y轴交于点A,作OC⊥AB于C,
如图,直线y=x+1与x轴交于点B,与y轴交于点A,作OC⊥AB于C,
则A(0,1),B(-1,0),
∵OA=OB=1,
∴△OAB为等腰直角三角形,
∴AB=
OA=
,
∵OC⊥AB,
∴OC=
AB=
,
∵直线y=x+1与⊙O相切,
∴OC为⊙O的半径,
∴圆O的半径为
.
故答案为
.
 如图,直线y=x+1与x轴交于点B,与y轴交于点A,作OC⊥AB于C,
如图,直线y=x+1与x轴交于点B,与y轴交于点A,作OC⊥AB于C,则A(0,1),B(-1,0),
∵OA=OB=1,
∴△OAB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
∵OC⊥AB,
∴OC=
| 1 |
| 2 |
| ||
| 2 |
∵直线y=x+1与⊙O相切,
∴OC为⊙O的半径,
∴圆O的半径为
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
把一个边长为3cm的正方形的各边长都增加x cm,则正方形增加的面积y(cm2)与x(cm)之间的函数表达式是( )
| A、y=(x+3)2 |
| B、y=x2+6x+6 |
| C、y=x2+6x |
| D、y=x2 |
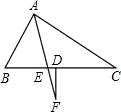 如图,AF平分∠BAC,FD⊥BD.
如图,AF平分∠BAC,FD⊥BD.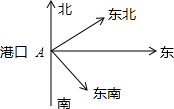 如图,一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?
如图,一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远? 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.
如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.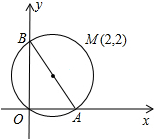 如图,过O和M(2,2)的⊙I,交坐标轴于A、B两点.
如图,过O和M(2,2)的⊙I,交坐标轴于A、B两点.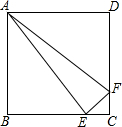 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.