Question

11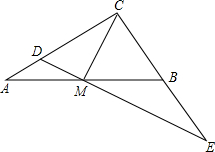．已知：如图，在△ABC中，∠ACB=90°，CM是斜边AB上的中线．
（1）过点M作CM的垂线与AC和BD的延长线分别交于点D和点E，求证：△CDM∽△ABC；
（2）过点M直线与AC和CB的延长线交于点D和点E，如果$\frac{DM}{MC}$=$\frac{AM}{ME}$，求证：CM⊥DE．

Answer 1

分析 （1）由在△ABC中，∠ACB=90°，CM是斜边AB的中线，根据直角三角形斜边的中线等于斜边的一半，可得CM=AM=BM=$\frac{1}{2}$AB，即可证得∠A=∠ACM，继而证得△CDM∽△ABC；
（2）根据已知条件得到$\frac{DM}{BM}=\frac{AM}{ME}$，由于∠AMD=∠BME，得到△ADM∽△BEM，根据相似三角形的性质得到∠A=∠E，等量代换得到∠E=∠ACM，求得∠E+∠ECM=90°，即可得到结论．

解答 证明：（1）∵在△ABC中，∠ACB=90°，CM是斜边AB的中线，
∴CM=AM=BM=$\frac{1}{2}$AB，
∴∠A=∠ACM，
∵CM⊥DE，
∴∠CMD=∠ACB=90°，
∴△CDM∽△ABC；

（2）∵$\frac{DM}{MC}$=$\frac{AM}{ME}$，CM=AM=BM，
∴$\frac{DM}{BM}=\frac{AM}{ME}$，
又∵∠AMD=∠BME，
∴△ADM∽△BEM，
∴∠A=∠E，
又∵∠A=∠ACM，
∴∠E=∠ACM，
又∵∠ACM+∠ECM=90°，
∴∠E+∠ECM=90°，
∴∠CME=90°，
∴CM⊥DB．

点评 此题考查了相似三角形的判定与性质、直角三角形斜边的中线的性质，垂直的定义，熟练掌握相似三角形的判定和性质是解题的关键．