题目内容
18.某农机租赁公司有30台农用车出租,若每车每天收费500元,可全部租出;若每车每天提价50元,则有1台车租不出去;若每车每天再提价50元,则又有1台车租不出去.按此市场行情推算,每车每天提价多少才能使该公司获得最大收益?最大收益为多少元?分析 设每车每天提价x元才能使该公司获得最大收益,利用租出的总台数×每车每天的收费=总收入列出函数解析式,利用配方法求得最值即可.
解答 解:设每车每天提价x元才能使该公司获得最大收益,总收益为y元,
则y=(500+x)(30-$\frac{x}{50}$)
=-$\frac{1}{50}$x2+20x+15000
=-$\frac{1}{50}$(x-500)2+20000
∵-$\frac{1}{50}$<0,
∴每车每天提价500元才能使该公司获得最大收益,最大收益为20000元.
点评 此题考查二次函数的实际运用,掌握题目蕴含的基本数量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.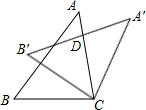 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )| A. | 48° | B. | 58° | C. | 68° | D. | 78° |
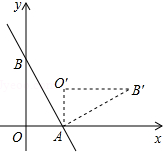 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标. 如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是旋转.
如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是旋转.