题目内容
6.某经销商销售的猕猴桃的进价是每千克5.7元,销售中约有5%的正常损耗.当销售价定为每千克9元时,每天可销售100千克,商家想采用提高销量的办法来增加利润,经试销发现:这种猕猴桃每千克的销售价每提高0.10元每天的销售量就下降10千克,且平均每天的其他成本为50元.(1)商家把猕猴桃的销售价至少定为每千克多少元时,才能避免亏本?
(2)求猕猴桃每天的销售量y(千克)与售价x(元/千克)之间的函数关系式.
(3)当猕猴桃销售价定为多少元时,才能使商家一天的利润最大?一天的最大利润时多少元?
分析 (1)把售价定为每千克x元,因为销售中估计有5%的猕猴桃正常损耗,故每千克猕猴桃损耗后的价格为x(1-5%),根据题意列出不等式即可;
(2)根据题意即可得到结论;
(3)设商家一天的利润为W元,根据题意得到二次函数关系式,二次函数的最大值即可.
解答 解:(1)设把售价定为每千克x元,
根据题意得:x(1-5%)≥5.7解得,x≥6,
故商家把售价至少定为6元,才能避免亏本;
(2)根据题意得:y=100-$\frac{x-9}{0.1}$×10=-100x+1000;
(3)设商家一天的利润为W元,
根据题意得:W=(-100x+1000)(x-5.7)×(1-5%)-50=-95x2+1491.5x-5465,
当x=7.85时,W最大=643.94.
故当猕猴桃销售价定为7.85元时,才能使商家一天的利润最大,一天的最大利润是643.94元.
点评 本题考查了二次函数的应用,由总利润=单个利润×数量建立函数关系式,二次函数的解析式的性质的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
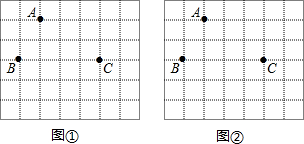
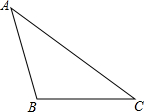 如图,已知△ABC,请按下列要求作图:
如图,已知△ABC,请按下列要求作图: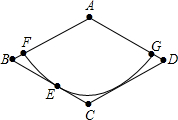 如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°.以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;
如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°.以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;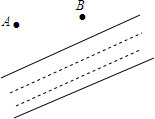 如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.
如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.