题目内容
7.数学课上,李老师出示了如下题目:在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图所示,试确定线段AE与DB的大小关系,并说明理由.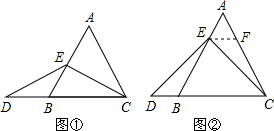
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB中点时,如图①,请你确定AE与DB的大小关系,并说明理由.
(2)特例启发,解决问题
当点E是AB上任一点时,AE与DB的大小关系是:AE=DB.
理由如下:如图②,过点E作EF∥BC,交AC于点F.(请你完成解答过程)
(3)拓展结论,设计新题
已知等边三角形ABC的边长为1,AE=2,且ED=EC.(请你直接写出下列结果)
①若点E在边AB的延长线上,点D在边CB的延长线上,则CD=3
②若点E在边BA的延长线上,点D在边BC的延长线上,则CD=1.
分析 (1)当E为中点时,过E作EF∥BC交AC于点F,则可证明△BDE≌△FEC,可得到AE=DB;
(2)类似(1)过E作EF∥BC交AC于点F,可利用AAS证明△BDE≌△FEC,可得BD=EF,再证明△AEF是等边三角形,可得到AE=EF,可得AE=DB;
(3)如图(4)或(5),作辅助线,证明△BDE≌△FEC,得到BD=EF;求出EF的长度,即可解决问题
解答 解:(1)如图1,过点E作EF∥BC,交AC于点F,
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,
$\left\{\begin{array}{l}{∠EBD=∠EFC}\\{∠EDB=∠FEC}\\{ED=EC}\end{array}\right.$,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD.
(2)如图2,过点E作EF∥BC,交AC于点F,
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,
$\left\{\begin{array}{l}{∠EBD=∠EFC}\\{∠EDB=∠FEC}\\{ED=EC}\end{array}\right.$,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
故答案为:=;
(3)如图4,当点E在AB的延长线上时,
过点E作EF∥BC,交AC的延长线于点F;
则∠DCE=∠CEF,∠DBE=∠AEF;
∠ABC=∠AEF,∠ACB=∠AFE;
∵△ACB为等边三角形,
∴∠ABC=∠ACB=60°,
∴∠AEF=∠AFE=60°,∠DBE=∠ABC=60°,
∴∠DBE=∠EFC;而ED=EC,
∴∠D=∠DCE,∠D=∠CEF;
在△BDE与△FEC中,
$\left\{\begin{array}{l}{∠D=∠CEF}\\{∠DBE=∠EFC}\\{DE=CE}\end{array}\right.$,
∴△BDE≌△FEC(AAS),
∴BD=EF;
∵△AEF为等边三角形,
∴AE=EF=2,BD=EF=2,
∴CD=1+2=3;
故答案为:3;
②如图5,当点E在BA的延长线上时
过点E作EF∥BC,交CA的延长线于点F;
类似上述解法,同理可证:DB=EF=2,BC=1
∴CD=2-1=1.
故答案为:1.
点评 本题主要考查全等三角形的判定和性质及等边三角形的性质和判定,利用全等得到BD=EF,再找EF和AE的关系是解题的关键.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
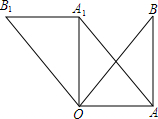 如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°