题目内容
1.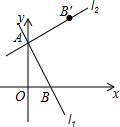 如图,直线11:y=-2x+2分别与x轴、y轴交于A、B点.将直线l1绕A点逆时针旋转90°,得到直线l2.
如图,直线11:y=-2x+2分别与x轴、y轴交于A、B点.将直线l1绕A点逆时针旋转90°,得到直线l2.(1)B点的对应点B′的坐标为(2,3);
(2)直线l2的解析式为y=$\frac{1}{2}$x+2.
分析 (1)令x=0求出A点坐标,令y=0即可求出B点的坐标然后证得△OAB≌△NAB′,易求点B′的坐标;
(2)设直线l2的解析式为y=kx+2,把B′(2,3)代入即可得出答案.
解答 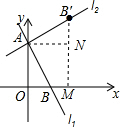 解:(1)∵直线11:y=-2x+2分别与x轴、y轴交于A、B点,
解:(1)∵直线11:y=-2x+2分别与x轴、y轴交于A、B点,
∴分别令y,x等于0,
解得A(0,2),B(1,0);
∴OA=2,OB=1,
作B′M⊥x轴于M,作AN⊥B′M于N,则四边形OANM是矩形,
∴MN=OA=2,
∵l1⊥l2,
∴∠BAN+∠B′AN=90°,
∵∠OAB+∠BAN=90°,
∴∠B′AN=∠OAB,
在△OAB和△NAB′中,
$\left\{\begin{array}{l}{∠AOB=∠ANB′=90°}\\{∠OAB=∠NAB′}\\{AB=AB′}\end{array}\right.$,
∴△OAB≌△NAB′(AAS),
∴OB=B′N=1,OA=AN=2,
∴B′M=2+1=3,
∴B'(2,3);
(2)设直线l2的解析式为y=kx+2,
把B′(2,3)代入得,3=2k+2,
解得k=$\frac{1}{2}$.
故直线l2的解析式为y=$\frac{1}{2}$x+2.
故答案为(2,3);y=$\frac{1}{2}$x+2.
点评 本题考查了一次函数的图象与几何变换,难度一般,关键是一次函数点的坐标的求法和解析式求法.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
9. 如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
 如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )| A. | 20海里 | B. | 40海里 | C. | 20$\sqrt{3}$海里 | D. | 40$\sqrt{3}$海里 |
 某市园林局准备种植A种花木4200棵,B种花木2400棵.现计划安排26人同时种植这两种花木,已知每人每天能种植A种花木30棵或B种花木20棵,则应分别安排多少人种植这两种花木,才能确保同时完成各自的任务?
某市园林局准备种植A种花木4200棵,B种花木2400棵.现计划安排26人同时种植这两种花木,已知每人每天能种植A种花木30棵或B种花木20棵,则应分别安排多少人种植这两种花木,才能确保同时完成各自的任务?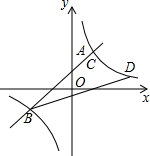 如图,一次函数y=kx+1(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,其中点A的坐标为(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点C,D.
如图,一次函数y=kx+1(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,其中点A的坐标为(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点C,D.