题目内容
16.若$\frac{a}{b}$=2,则$\frac{{a}^{2}+ab}{{a}^{2}-{b}^{2}}$的值为2.分析 根据等式的性质,可用b表示a,根据分式的性质,可得答案.
解答 解:由$\frac{a}{b}$=2,得a=2b.
$\frac{{a}^{2}+ab}{{a}^{2}-{b}^{2}}$=$\frac{4{b}^{2}+2{b}^{2}}{4{b}^{2}-{b}^{2}}$=2,
故答案为:2.
点评 本题考查了比例的性质,利用等式的性质得出a=2b是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
6. 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
4.-3+(-5)×(-1)的结果是( )
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
11.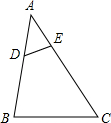 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )| A. | 5 | B. | 12.5 | C. | 25 | D. | $\sqrt{21}$ |
11.甲乙两校九年级学生英语听力的测试情况如下表所示:
(每小组中的数据可含最低值,不含最高值)
(1)补填表格内的频率.
(2)画出两校九年级学生英语听力的测试成绩的频率分布直方图.
(3)比较两校九年级学生听力的测试成绩.
| 成绩 | 甲校 | 乙校 | ||
| 频数 | 频率 | 频数 | 频率 | |
| 不合格 40分~60分 | 3 | $\frac{3}{205}$ | 1 | $\frac{1}{108}$ |
| 合格 60~80分 | 166 | $\frac{166}{205}$ | 82 | $\frac{41}{54}$ |
| 优良 80分~100分 | 36 | $\frac{36}{205}$ | 25 | $\frac{25}{108}$ |
| 合计 | 205 | 1 | 108 | 1 |
(1)补填表格内的频率.
(2)画出两校九年级学生英语听力的测试成绩的频率分布直方图.
(3)比较两校九年级学生听力的测试成绩.
 如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)
如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)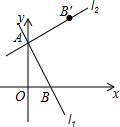 如图,直线11:y=-2x+2分别与x轴、y轴交于A、B点.将直线l1绕A点逆时针旋转90°,得到直线l2.
如图,直线11:y=-2x+2分别与x轴、y轴交于A、B点.将直线l1绕A点逆时针旋转90°,得到直线l2.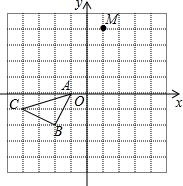 如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.