题目内容
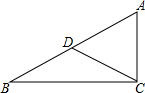 如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.
如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.考点:解直角三角形
专题:
分析:先由三角形外角的性质得出∠ADC=∠B+∠BCD,而∠ADC=2∠B,那么∠B=∠BCD,根据等角对等边得出BD=CD=3.由∠B+∠A=∠BCD+∠ACD=90°,得到∠A=∠ACD,根据等角对等边得出AD=CD=3,那么AB=AD+BD=6.然后在Rt△ABC中,根据勾股定理求出BC=
=2
,再利用正切函数的定义即可求出tan∠B.
| 62-42 |
| 5 |
解答:解:∵∠ADC=∠B+∠BCD,∠ADC=2∠B,
∴∠B=∠BCD,
∴BD=CD=3.
∵∠B+∠A=∠BCD+∠ACD=90°,
∴∠A=∠ACD,
∴AD=CD=3,
∴AB=AD+BD=3+3=6.
在Rt△ABC中,∵∠ACB=90°,AB=6,AC=4,
∴BC=
=2
,
∴tan∠B=
=
=
.
∴∠B=∠BCD,
∴BD=CD=3.
∵∠B+∠A=∠BCD+∠ACD=90°,
∴∠A=∠ACD,
∴AD=CD=3,
∴AB=AD+BD=3+3=6.
在Rt△ABC中,∵∠ACB=90°,AB=6,AC=4,
∴BC=
| 62-42 |
| 5 |
∴tan∠B=
| AC |
| BC |
| 4 | ||
2
|
2
| ||
| 5 |
点评:本题考查了解直角三角形,三角形外角的性质,等腰三角形的判定,勾股定理,锐角三角函数的定义,难度适中.求出AB的长是解题的关键.

练习册系列答案
相关题目
下列数组中,不是勾股数的是( )
| A、5、12、13 |
| B、11、13、15 |
| C、15、20、25 |
| D、7、24、25 |
 △ABC在直角坐标系中的位置如图所示,∠C=90°,点C的坐标为(
△ABC在直角坐标系中的位置如图所示,∠C=90°,点C的坐标为(| 3 |
| 2 |
| ||
| 2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,0) |
在Rt△ACB中,∠C=90°,sinB=
,则tanA=( )
| 1 |
| 5 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、24 |
 如图,∠COB=2∠AOC,OD平分∠AOB,∠AOB=114°,求∠COD的度数.
如图,∠COB=2∠AOC,OD平分∠AOB,∠AOB=114°,求∠COD的度数.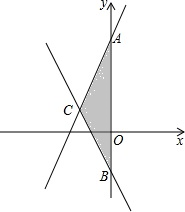 如图,已知直线y=2x+5和y=-x-1相交于点C,且两直线与y轴的交点分别是A,B.
如图,已知直线y=2x+5和y=-x-1相交于点C,且两直线与y轴的交点分别是A,B.