题目内容

12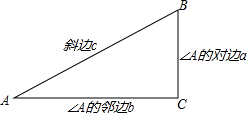．如图，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别是a、b、c，我们把∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cosA=$\frac{b}{c}$．当c=2，a=1时，求cosA．

分析 根据勾股定理求出b，根据余弦的定义计算即可．

解答 解：∵∠C=90°，c=2，a=1，
∴b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$，
∴cosA=$\frac{b}{c}$=$\frac{\sqrt{3}}{2}$．

点评 本题考查的是锐角三角函数的定义，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

练习册系列答案
相关题目
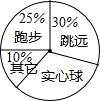2．学校为了今年初三年级学生体育中考取得优异的成绩，进行更有针对性的强化训练，体育组为了了解学生最喜欢的考试项目情况，随机抽查了该年级200名学生，调查的结果如图所示．
（1）请根据该扇形统计图解答以下问题：
①最喜欢跳远考试项目的学生人数有60人．
②求表示喜欢实心球考试项目的扇形圆心角的度数．
（2）该校从初三年级选3名学生代表去选训练运动服，现有三套运动服，有三件颜色分别为红、黄、蓝的上衣和两条蓝色、一条白色的裤子，请利用树形图或列表方法求出上衣和裤子均为蓝色的概率．
3．在直线l上找到一点P使它到A、B两点的距离相等（尺规作图，保留作图痕迹）
20．解方程（组）：
（1）$\frac{2}{x-1}$-$\frac{x+2}{x-1}$=1         
（2）$\left\{\begin{array}{l}3x+2y=15\\ 7x+2y=27\end{array}$．
7．如图，△ABC中，BE是它的角平分线，∠C=90°，D在AB边上，以DB为直径的半圆O经过点E，交BC于点F．
（1）求证：AC是⊙O的切线．
（2）若∠C=30°，连接EF，求证：EF∥AB；
（3）在（2）的条件下，若AE=2$\sqrt{3}$，求图中阴影部分的面积．
17．函数$y=（m-1）{x^{{m^2}-2}}$是反比例函数，则m的值是（　　）
A．m=±1B．m=1C．m=±$\sqrt{3}$D．m=-1
4．春节期间，小刚随爸爸从陇南来兰州游玩，由于仅有一天的时间，小刚不能游玩所有风景区，于是爸爸让小刚上午从A：兰州极地海洋世界（收费），B：白塔山公园（免费），C：水车博览园（免费）中任意选择一处游玩；下午从D：五泉山公园（免费），E：安宁滑雪场（收费），F：甘肃省博物馆（免费），G：西部欢乐园（收费）中任意选一处游玩．
（1）请用树状图或列表法说明小刚所有可能选择的方式（用字母表示）；
（2）求小刚这一天游玩的景点恰好是免费的概率．
1．计算：
（1）$\sqrt{16}$-$\sqrt{9}$+$\root{3}{-27}$
（2）|2-$\sqrt{3}$|+2（$\sqrt{3}$-1）
（3）$\sqrt{\frac{1}{16}}$-$\sqrt{6\frac{1}{4}}$+|$\sqrt{3}$-π|+$\sqrt{3}$
（4）$\sqrt{4}$÷2+$\root{3}{27}$×[2-（-$\sqrt{2}$）2]．
2．计算下列各题：
（1）计算|-$\sqrt{12}$|+（$\frac{1}{2}$）-1-（1+$\sqrt{3}$）0+2•tan60°
（2）解不等式组：$\left\{\begin{array}{l}-2x+1＜3x-4\\ \frac{1}{3}≥\frac{x-2}{2}-\frac{x}{3}\end{array}$并将不等式组的解集在数轴上表示出来．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网