题目内容
2.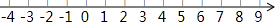 计算下列各题:
计算下列各题:(1)计算|-$\sqrt{12}$|+($\frac{1}{2}$)-1-(1+$\sqrt{3}$)0+2•tan60°
(2)解不等式组:$\left\{\begin{array}{l}-2x+1<3x-4\\ \frac{1}{3}≥\frac{x-2}{2}-\frac{x}{3}\end{array}$并将不等式组的解集在数轴上表示出来.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)原式=|-2$\sqrt{3}$|+2-1+2×$\sqrt{3}$
=2$\sqrt{3}$+1+2$\sqrt{3}$
=4$\sqrt{3}$+1;
(2)$\left\{\begin{array}{l}-2x+1<3x-4①\\ \frac{1}{3}≥\frac{x-2}{2}-\frac{x}{3}②\end{array}\right.$,由①得x>1,由②得x≤8,
所以不等式组的解集是:1<x≤8.
在数轴上表示为: .
.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的计算法则、特殊角的三角函数值是解答此题的关键.

练习册系列答案
相关题目
17.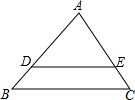 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )| A. | 6 | B. | 4.5 | C. | 2 | D. | 1.5 |
7.下列计算正确的是( )
| A. | x3•x4=x12 | B. | 4x4÷2x2=2x2 | C. | |a|=a | D. | (-xy2)3=x3y6 |
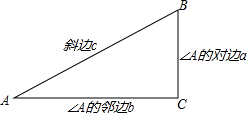 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=$\frac{b}{c}$.当c=2,a=1时,求cosA.
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=$\frac{b}{c}$.当c=2,a=1时,求cosA. 如图,在四边形ABCD中,点M、N、P分别是AD、BC、BD的中点,如果$\overrightarrow{BA}=\vec a,\overrightarrow{DC}=\vec b$,那么$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\vec a和\vec b$表示)
如图,在四边形ABCD中,点M、N、P分别是AD、BC、BD的中点,如果$\overrightarrow{BA}=\vec a,\overrightarrow{DC}=\vec b$,那么$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\vec a和\vec b$表示)