题目内容
7. 如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.(1)求证:AC是⊙O的切线.
(2)若∠C=30°,连接EF,求证:EF∥AB;
(3)在(2)的条件下,若AE=2$\sqrt{3}$,求图中阴影部分的面积.
分析 (1)利用平行线的性质结合等腰三角形的性质得出∠BEO=∠CBE,进而得出∠AEO=∠C=90°,即可得出答案;
(2)根据已知得出∠CEF=∠FBE=30°,进而得出∠BEF的度数,得出∠BEF=∠OBE,进而得出答案;
(3)得出S△EFB=S△EOF,由S阴影=S扇EOF,求出答案.
解答 (1)证明:连接OE,
∵OB=OE,
∴∠BEO=∠EBO,
∵BE平分∠CBO,
∴∠EBO=∠CBE,
∴∠BEO=∠CBE,
∴EO∥BC,
∵∠C=90°,
∴∠AEO=∠C=90°,
则AC是圆O的切线;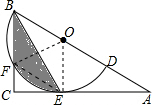
(2)证明:∵∠A=30°,
∴∠ABC=60°,
∴∠OBE=∠FBE=30°,
∴∠BEC=90°-∠FBE=60°,
∵∠CEF=∠FBE=30°,
∴∠BEF=∠BEC-∠CEF=60°-30°=30°,
∴∠BEF=∠OBE,
∴EF∥AB;
(3)解:连接OF
∵EF∥AB,
∴S△EFB=S△EOF,
∴S阴影=S扇EOF,
设圆的半径为r,在Rt△AEO中,r=2,
∴S阴影=S扇EOF=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$.
点评 此题主要考查了切线的判定以及扇形面积求法、平行线的判定与性质等知识,正确作出辅助线得出S阴影=S扇EOF是解题关键.

练习册系列答案
相关题目
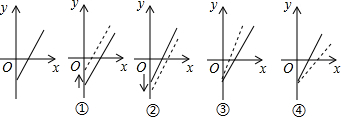
15.如图是小李销售某种食品的总利润y元与销售量x千克的函数图象(总利润=总销售额-总成本).由于目前销售不佳,小李想了两个解决方案:
方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )
方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )

| A. | ②,③ | B. | ①,③ | C. | ①,④ | D. | ④,② |
16.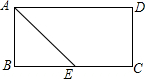 在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
 在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )| A. | 2和3 | B. | 3和2 | C. | 4和1 | D. | 1和4 |
17.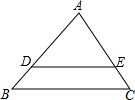 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )| A. | 6 | B. | 4.5 | C. | 2 | D. | 1.5 |
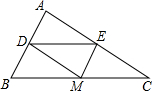 如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是4.8cm.
如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是4.8cm.
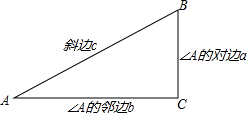 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=$\frac{b}{c}$.当c=2,a=1时,求cosA.
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=$\frac{b}{c}$.当c=2,a=1时,求cosA.