题目内容
8.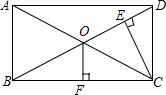 如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
分析 由矩形的性质得出OC=OD=OA=OB,证出OF是△ABC的中位线,得出CD=AB=2OF=72cm,再证出CE是线段OD的垂直平分线,得出OC=CD,得出OC=OD=CD=72cm,即可求出AC的长.
解答 解:∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,AB⊥BC,
∴OC=OD=OA=OB,
∵OF⊥BC,
∴OF∥AB,
∴OF是△ABC的中位线,
∴CD=AB=2OF=72cm,
∵BE=3DE,
∴OE=DE,
∵CE⊥OD,
∴OC=CD,
∴OC=OD=CD=72cm,
∴AC=2OA=144cm.
点评 本题考查了矩形的性质、三角形中位线定理、等边三角形的判定;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
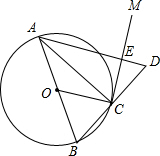 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.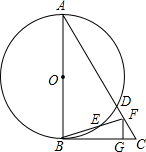 如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
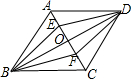 如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )
如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( ) 如图,线段AB与CD相交于点O,OA=OC,还需增加一个条件,OD=OB,使得△AOD≌△COB.
如图,线段AB与CD相交于点O,OA=OC,还需增加一个条件,OD=OB,使得△AOD≌△COB. 如图,在△ABC中,BE⊥AC于点E,CF⊥AB于点F,D为BC边的中点,连接DE,DF.
如图,在△ABC中,BE⊥AC于点E,CF⊥AB于点F,D为BC边的中点,连接DE,DF. 已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点,求证:AB2=AD•AE.
已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点,求证:AB2=AD•AE.