题目内容
3.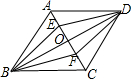 如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )
如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点,易证得四边形BFDE是菱形,△DEF是等腰三角形,即可判定B,D正确;又由等底等高三角形的面积相等,即可判定A正确,继而求得答案.
解答 解:A、∵E是OA的中点,
∴AE=OE,
∵△ADE与△EOD等高,
∴S△ADE=S△EOD,
故本选项正确;
B、∵四边形ABCD是菱形,
∴OA=OC,OB=OD,
∵E、F分别是OA、OC的中点,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴四边形BFDE是中心对称图形;
故本选项正确;
C、∵OE=OF,AC⊥BD,
∴△DEF是等腰三角形,
∴△DEF是轴对称图形;
故本选项正确;
D、∵AD>OD,AE=OE,
∴∠ADE≠∠ODE,
故本选项错误.
∴正确的结论有3个,
故选C.
点评 此题考查了菱形的性质与判定、轴对称性与中心对称性.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
13.下列大学的校徽图案是轴对称图形的是( )
| A. |  浙江大学 | B. |  北京大学 | C. |  中国人民大学 | D. |  清华大学 |
14.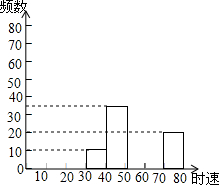 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
| 时速x(km/h) | 频 数 | 频 率 |
| 30≤x≤40 | 10 | 0.05 |
| 40≤x≤50 | 36 | 0.18 |
| 50≤x≤60 | 78 | 0.39 |
| 60≤x≤70 | 56 | 0.28 |
| 70≤x≤80 | 20 | 0.10 |
| 总 计 | 200 | 1 |
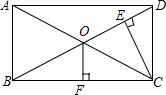 如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.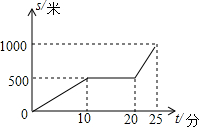 某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,如图是王老师从家到学校这一过程中的所有路程s(米)与时间t(分)之间的关系.
某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,如图是王老师从家到学校这一过程中的所有路程s(米)与时间t(分)之间的关系.