题目内容
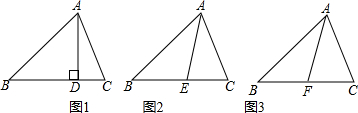
17. 已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点,求证:AB2=AD•AE.
已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点,求证:AB2=AD•AE.
分析 连接BE,由圆周角定理可知∠E=∠C,根据等腰三角形的性质可知∠ABC=∠C,所以∠E=∠ABC,再加公共角相等即可证明△ABE∽△ADB,利用相似三角形的性质即可得到AB2=AD•AE;
解答  证明:连接BE,
证明:连接BE,
∴∠E=∠C,
∵AB=AC,
∴∠ABC=∠C,
∴∠E=∠ABC,
∵∠BAE=∠DAB,
∴△ABE∽△ADB,
∴AB:AD=AE:AB,
∴AB2=AD•AE.
点评 本题考查了等腰三角形的性质、相似三角形的判定和性质以及圆周角定理,题目的综合性较强,难度中等.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
9.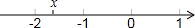 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
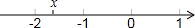 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )| A. | x0>x-1>x-2>x-4 | B. | x-4>x-2>x-1>x0 | C. | x-2>x-4>x0>x-1 | D. | x0>x-2>x-4>x-1 |
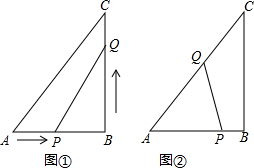
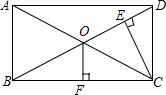 如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长. 如图,是我国体育健儿在最近六届奥运会上获得奖牌的情况,那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚.
如图,是我国体育健儿在最近六届奥运会上获得奖牌的情况,那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚.
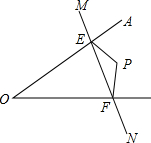 如图,点P在∠AOB内部,点M,N分别是点P关于直线AO、BO的对称点,若△PEF的周长为15,求MN的长.
如图,点P在∠AOB内部,点M,N分别是点P关于直线AO、BO的对称点,若△PEF的周长为15,求MN的长.