题目内容
18.用代入法解下列方程组.(1)$\left\{\begin{array}{l}{3x+4y=16}\\{5x-6y=33}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=6}\\{4(x+y)-5(x-y)=2}\end{array}\right.$.
分析 (1)①×3+②×2得出19x=114,求出x,把x的值代入①求出y即可;
(2)设x+y=a,x-y=b,原方程组化为$\left\{\begin{array}{l}{3a+2b=36}\\{4a-5b=2}\end{array}\right.$,求出a、b的值,得出关于x、y的方程组,求出方程组的解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+4y=16①}\\{5x-6y=33②}\end{array}\right.$
①×3+②×2得:19x=114,
解得:x=6,
把x=6代入①得:18+4y=16,
解得:y=-$\frac{1}{2}$.
所以原方程组的解为:$\left\{\begin{array}{l}{x=6}\\{y=-\frac{1}{2}}\end{array}\right.$;
(2)设x+y=a,x-y=b,
原方程组化为:$\left\{\begin{array}{l}{3a+2b=36}\\{4a-5b=2}\end{array}\right.$,
解得:a=8,b=6,
即$\left\{\begin{array}{l}{x+y=8}\\{x-y=6}\end{array}\right.$,
解得:x=7,y=1.
所以原方程组的解为:$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$.
点评 本题考查了解二元一次方程组的应用,能把二元一次方程组转化成一元一次方程是解此题的关键,解二元一次方程组的方法有:代入法和加减法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.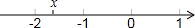 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
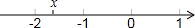 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )| A. | x0>x-1>x-2>x-4 | B. | x-4>x-2>x-1>x0 | C. | x-2>x-4>x0>x-1 | D. | x0>x-2>x-4>x-1 |
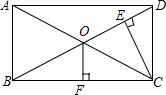 如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
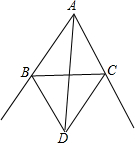 如图,已知,△ABC的∠B,∠C的外角平分线交于点D,AD是∠BAC的平分线吗?说明理由.
如图,已知,△ABC的∠B,∠C的外角平分线交于点D,AD是∠BAC的平分线吗?说明理由.
 如图,AB∥CD,AC⊥CE,∠BAE=3∠DCE,∠E=54°,求∠BAC的度数.
如图,AB∥CD,AC⊥CE,∠BAE=3∠DCE,∠E=54°,求∠BAC的度数.